题目内容
顶点在原点,经过圆C:x2+y2-2x+2
y=0的圆心且准线与x轴垂直的抛物线方程为( )
| 2 |
| A、y2=-2x | ||
| B、y2=2x | ||
C、y=
| ||
D、y=-
|
考点:抛物线的标准方程,圆的一般方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:设出抛物线方程,利用经过点(1,-
),求出抛物线中的参数,即可得到抛物线方程.
| 2 |
解答:
解:因为圆C:x2+y2-2x+2
y=0的圆心是(1,-
)
抛物线的顶点在原点,焦点在x轴上,且经过点(1,-
),
设标准方程为y2=2px,
因为点(1,-
)在抛物线上,所以(-
)2=2p,
所以p=1,
所以所求抛物线方程为:y2=2x.
故选:B.
| 2 |
| 2 |
抛物线的顶点在原点,焦点在x轴上,且经过点(1,-
| 2 |
设标准方程为y2=2px,
因为点(1,-
| 2 |
| 2 |
所以p=1,
所以所求抛物线方程为:y2=2x.
故选:B.
点评:本题考查抛物线的标准方程的求法,注意标准方程的形式,考查计算能力,是易错题,基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
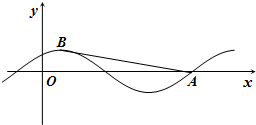 已知函数f(x)=2
已知函数f(x)=2 已知函数:y=x2,y=log2x,y=2x,y=sinx,y=cosx,y=tanx.从中选出两个函数记为f(x)和g(x),若F(x)=f(x)+g(x)的图象如图所示,则F(x)=
已知函数:y=x2,y=log2x,y=2x,y=sinx,y=cosx,y=tanx.从中选出两个函数记为f(x)和g(x),若F(x)=f(x)+g(x)的图象如图所示,则F(x)=