题目内容
4.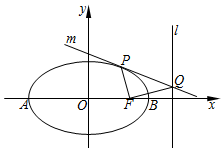 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右顶点分别为A、B,它的右焦点是F(1,0).椭圆上一动点P(x0,y0)(不是顶点)满足${k_{PA}}•{k_{PB}}=-\frac{1}{2}$.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右顶点分别为A、B,它的右焦点是F(1,0).椭圆上一动点P(x0,y0)(不是顶点)满足${k_{PA}}•{k_{PB}}=-\frac{1}{2}$.(1)求椭圆的方程;
(2)设过点P且与椭圆相切的直线为m,直线m与椭圆的右准线l交于点Q,试证明∠PFQ为定值.
分析 (1)由题意可知:根据直线的斜率公式求得$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,c=1,则a2-b2=1,即可求得a和b的值,求得椭圆方程;
(2)设直线l的方程,代入椭圆方程,由△=0,求得k和t的关系,代入求得P点坐标,则椭圆的准线方程,求得Q点坐标,即可求得$\overrightarrow{FQ}$•$\overrightarrow{FP}$=0,则∠PFQ为定值.
解答 解:(1)由P(x0,y0),则y02=$\frac{{{b}^{2}(a}^{2}-{x}_{0}^{2})}{{a}^{2}}$
kPA•kPB=$\frac{{y}_{0}-0}{{x}_{0}+a}$•$\frac{{y}_{0}-0}{{x}_{0}-a}$=$\frac{{y}_{0}^{2}}{{x}_{0}^{2}-{a}^{2}}$=-$\frac{{b}^{2}}{{a}^{2}}$,
则${k_{PA}}•{k_{PB}}=-\frac{1}{2}$.则$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,①
由c=1,则a2-b2=1,②
解得:a2=2,b2=1,
∴椭圆的标准方程:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)证明:设直线PQ的方程,y=kx+t,
则$\left\{\begin{array}{l}{y=kx+t}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:(1+2k2)x2+4ktx+2t2-2=0,
则△=(4kt)2-4(1+2k2)(2t2-2)=0,解得:t2=1+2k2,即t=±$\sqrt{1+2{k}^{2}}$,
∴(1+2k2)x2+4k$\sqrt{1+2{k}^{2}}$x+4k2=0,
解得:x=$\frac{-2k\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$,
将x=$\frac{-2k\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$,代入椭圆方程,解得:y=±$\frac{\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$,
则P($\frac{-2k\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$,$\frac{\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$),或P($\frac{-2k\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$,-$\frac{\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$),
椭圆的准线方程x=$\frac{{a}^{2}}{c}$=2,
将x=2代入y=kx+t,y=2k+$\sqrt{1+2{k}^{2}}$,即Q(2,2k+$\sqrt{1+2{k}^{2}}$),
F(1,0),P($\frac{-2k\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$,$\frac{\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$),Q(2,2k+$\sqrt{1+2{k}^{2}}$),
∴$\overrightarrow{FQ}$=(1,2k+$\sqrt{1+2{k}^{2}}$),$\overrightarrow{FP}$=($\frac{-2k\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$-1,$\frac{\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$),
则$\overrightarrow{FQ}$•$\overrightarrow{FP}$=($\frac{-2k\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$-1)(2k+$\sqrt{1+2{k}^{2}}$)×$\frac{\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$=0,
同理:将x=2代入y=kx-t,y=2k-$\sqrt{1+2{k}^{2}}$,即Q(2,2k-$\sqrt{1+2{k}^{2}}$),
∴P($\frac{-2k\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$,-$\frac{\sqrt{1+2{k}^{2}}}{1+2{k}^{2}}$),Q(2,2k-$\sqrt{1+2{k}^{2}}$),F(1,0),$\overrightarrow{FQ}$•$\overrightarrow{FP}$=0,
即$\overrightarrow{FQ}$⊥$\overrightarrow{FP}$,
综上可知:$\overrightarrow{FQ}$•$\overrightarrow{FP}$=0,$\overrightarrow{FQ}$⊥$\overrightarrow{FP}$,
∴∠PFQ=90°为定值.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,向量数量积的坐标运算,属于中档题.

| A. | B*D,A*D | B. | B*D,A*C | C. | B*C,A*D | D. | C*D,A*D |