题目内容
15.已知α是△ABC的一个内角,且$sinα+cosα=\frac{1}{5}$,(Ⅰ)判断△ABC的形状;
(Ⅱ)求sinα-cosα的值.
分析 (Ⅰ)把所给的等式平方可得 sinαcosα=-$\frac{12}{25}$<0,可得α为钝角,故△ABC为钝角三角形.
(Ⅱ)由(Ⅰ)可得sinα-cosα=$\sqrt{{(sinα-cosα)}^{2}}$,计算求得结果.
解答 解:(Ⅰ)∵α是△ABC的一个内角,且$sinα+cosα=\frac{1}{5}$,
∴平方可得1+2sinαcosα=$\frac{1}{25}$,∴sinαcosα=-$\frac{12}{25}$<0,
∴α为钝角,故△ABC为钝角三角形.
(Ⅱ)由以上可得sinα-cosα=$\sqrt{{(sinα-cosα)}^{2}}$=$\sqrt{1-2sinαcosα}$=$\sqrt{\frac{49}{25}}$=$\frac{7}{5}$.
点评 本题主要考查同角三角函数的基本关系的应用,二倍角公式,属于基础题.

练习册系列答案
相关题目
5.如果直线 l 经过两直线2x-3y+1=0和3x-y-2=0的交点,且与直线y=x垂直,则原点到直线 l 的距离是( )
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
6.数列{an}的前n项和为Sn,若Sn=2n-1(n∈N+),则a2017的值为( )
| A. | 2 | B. | 3 | C. | 2017 | D. | 3033 |
10.sin4cos3tan2的值为( )
| A. | 负数 | B. | 正数 | C. | 0 | D. | 不存在 |
7.已知角α的顶点在原点,始边与x轴的正半轴重合
(1)若终边经过点P(-1,2),求sin αcos α的值;
(2)若角α的终边在直线y=-3x上,求tan α+$\frac{3}{cosα}$的值.
(1)若终边经过点P(-1,2),求sin αcos α的值;
(2)若角α的终边在直线y=-3x上,求tan α+$\frac{3}{cosα}$的值.
5.取一根长为3m的绳子AB,拉直后在任意位置C剪断,那么满足AC-BC≥1的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
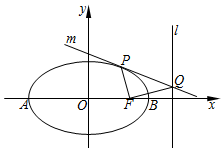 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右顶点分别为A、B,它的右焦点是F(1,0).椭圆上一动点P(x0,y0)(不是顶点)满足${k_{PA}}•{k_{PB}}=-\frac{1}{2}$.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右顶点分别为A、B,它的右焦点是F(1,0).椭圆上一动点P(x0,y0)(不是顶点)满足${k_{PA}}•{k_{PB}}=-\frac{1}{2}$.