题目内容
13.甲袋中放有大小和形状相同的小球若干,其中标号为0的小球为1个,标号为1的小球2个,标号为2的小球2个.从袋中任取两个球,已知其中一个的标号是1,则另一个标号也是1的概率为$\frac{1}{7}$.分析 记“一个标号是1”为事件A,“另一个标号也是1”为事件B,求出P(A)=$\frac{7}{10}$,P(AB)=$\frac{1}{10}$,从袋中任取两个球,已知其中一个的标号是1,利用条件概率计算公式能求出另一个标号也是1的概率.
解答 解:记“一个标号是1”为事件A,
“另一个标号也是1”为事件B,
P(A)=$\frac{{C}_{2}^{1}{C}_{3}^{1}+{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{7}{10}$,
P(AB)=$\frac{{C}_{2}^{2}}{{C}_{5}^{2}}$=$\frac{1}{10}$,
∴从袋中任取两个球,已知其中一个的标号是1,
另一个标号也是1的概率P(A|B)=$\frac{P(AB)}{P(A)}$=$\frac{\frac{1}{10}}{\frac{7}{10}}$=$\frac{1}{7}$.
故答案为:$\frac{1}{7}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意条件概率计算公式的合理运用.

练习册系列答案
相关题目
18.已知随机变量X服从正态分布N(100,532),P(X<110)=0.84,则P(90<X≤100)=( )
| A. | 0.16 | B. | 0.34 | C. | 0.42 | D. | 0.84 |
5.取一根长为3m的绳子AB,拉直后在任意位置C剪断,那么满足AC-BC≥1的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
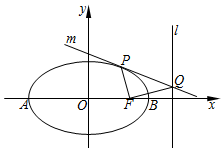 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右顶点分别为A、B,它的右焦点是F(1,0).椭圆上一动点P(x0,y0)(不是顶点)满足${k_{PA}}•{k_{PB}}=-\frac{1}{2}$.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右顶点分别为A、B,它的右焦点是F(1,0).椭圆上一动点P(x0,y0)(不是顶点)满足${k_{PA}}•{k_{PB}}=-\frac{1}{2}$.