题目内容

14．3位男生和3位女生共6位同学站成一排，若3位女生中有且只有两位女生相邻，则不同排法的种数是432．

分析 从3名女生中任取2人“捆”在一起记作A，剩下一名女生记作B，将A，B插入到3名男生全排列后所成的4个空中的2个空中，问题得以解决．

解答 解：从3名女生中任取2人“捆”在一起记作A，（A共有C32A22=6种不同排法），剩下一名女生记作B，
将A，B插入到3名男生全排列后所成的4个空中的2个空中，故有C32A22A42A33=432种，
故答案为：432

点评 本题考查排列组合的运用，当题目中有限制的条件有两个，注意解题时要分清两个条件所指．

练习册系列答案
相关题目
4．一个袋中装有大小相同，编号分别为1，2，3，4，5，6，7，8的八个球，从中有放回地每次取一个球，共取2次，则取得两个球的编号和小于15的概率为（　　）
A．$\frac{29}{32}$B．$\frac{63}{64}$C．$\frac{31}{32}$D．$\frac{61}{64}$
5．如果直线 l 经过两直线2x-3y+1=0和3x-y-2=0的交点，且与直线y=x垂直，则原点到直线 l 的距离是（　　）
A．2B．1C．$\sqrt{2}$D．2$\sqrt{2}$
2．关于函数f（x）=4sin（2x+$\frac{π}{3}$）（x∈R），有下列说法：
①函数y=f（x）的图象向右平移$\frac{π}{3}$个单位后得到的图象关于原点对称；
②函数y=f（x）是以2π为最小正周期的周期函数；
③函数y=f（x）的图象关于点$（{-\frac{π}{6}，0}）$对称；
④函数y=f（x）的图象关于直线x=$\frac{π}{6}$对称．
其中正确的是③．（填上所有你认为正确的序号）
9．将时钟拨慢了15分钟，则分针转过的弧度数是$\frac{π}{2}$．
19．在平面直角坐标系xoy中，点P到$（{0，-\sqrt{3}}），（{0，\sqrt{3}}）$两点的距离之和等于4，若点P的轨迹为C．
（1）求C的方程；
（2）如果经过点（0，1）的直线l交C于点A，B，且$\overrightarrow{OA}•\overrightarrow{AB}=0$，求该直线的方程及$|{\overrightarrow{AB}}|$．
6．数列{an}的前n项和为Sn，若Sn=2n-1（n∈N+），则a2017的值为（　　）
A．2B．3C．2017D．3033
3．已知等差数列{an}中，a1=-60，a17=-12．
（1）该数列第几项起为正？
（2）前多少项和最小？求数列{an}的前n项和Sn的最小值
（3）设Tn=|a1|+|a2|+|a3|+…+|an|
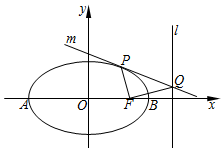4．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右顶点分别为A、B，它的右焦点是F（1，0）．椭圆上一动点P（x0，y0）（不是顶点）满足${k_{PA}}•{k_{PB}}=-\frac{1}{2}$．
（1）求椭圆的方程；
（2）设过点P且与椭圆相切的直线为m，直线m与椭圆的右准线l交于点Q，试证明∠PFQ为定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网