题目内容
12．在锐角三角形ABC中，a，b，c分别是角A，B，C的对边，且a=2bsinA．（1）求∠B的大小；
（2）若a=3$\sqrt{3}$，c=5，求三角形ABC的面积和b的值．
分析 （1）由正弦定理化a=2bsinA为sinA=2sinBsinA，求出sinB的值即得B的大小；
（2）由余弦定理求出b的值，利用三角形的面积公式求出S△ABC．
解答 解：（1）锐角△ABC中，a=2bsinA，
∴sinA=2sinBsinA，
解得sinB=$\frac{1}{2}$；
又B为锐角，
∴B=30°；
（2）由a=3$\sqrt{3}$，c=5，
∴b2=a2+c2-2accosB
=${（3\sqrt{3}）}^{2}$+52-2×3$\sqrt{3}$×5×cos30°
=7，
∴$b=\sqrt{7}$；
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{1}{2}$×3$\sqrt{3}$×5×sin30°=$\frac{15\sqrt{3}}{4}$．
点评 本题考查了正弦、余弦定理和三角形面积公式的应用问题，是基础题．
练习册系列答案
提分百分百检测卷系列答案
相关题目
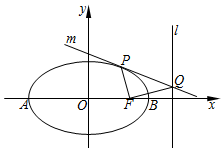已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右顶点分别为A、B，它的右焦点是F（1，0）．椭圆上一动点P（x0，y0）（不是顶点）满足${k_{PA}}•{k_{PB}}=-\frac{1}{2}$．
