题目内容
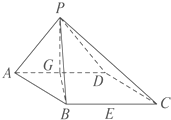 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.(1)求证:BG⊥平面PAD;
(2)求平面PBG与平面PCD所成二面角的平面角的余弦值;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
考点:平面与平面垂直的判定,直线与平面垂直的判定,与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间角
分析:(1)连结BD,由正三角形性质的BG⊥AD,由此能证明BG⊥平面PAD.
(2)以G为原点,建立空间直角坐标系G-xyz,由此能求出平面PBG与平面PCD所成二面角的平面角的余弦值.
(3)当F为PC的中点时,平面DEF⊥平面ABCD.取PC的中点F,连结DE,EF,DF,CG,且DE与CG相交于H,由已知条件得四边形CDGE为平行四边形,由此能证明平面DEF⊥平面ABCD.
(2)以G为原点,建立空间直角坐标系G-xyz,由此能求出平面PBG与平面PCD所成二面角的平面角的余弦值.
(3)当F为PC的中点时,平面DEF⊥平面ABCD.取PC的中点F,连结DE,EF,DF,CG,且DE与CG相交于H,由已知条件得四边形CDGE为平行四边形,由此能证明平面DEF⊥平面ABCD.
解答:
(本小题满分14分)
(1)证明:连结BD.
因为ABCD为棱形,且∠DAB=60°,
所以△ABD为正三角形.(1分)
又G为AD的中点,所以BG⊥AD.(2分)
又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,(3分)
∴BG⊥平面PAD.(4分)
(2)解:∵△PAD为正三角形,G为AD的中点,∴PG⊥AD.
∵PG?平面PAD,由(1)得:PG⊥GB.又由(1)知BG⊥AD.
∴PG、BG、AD两两垂直.(5分)
故以G为原点,建立如图所示空间直角坐标系G-xyz,
PG=PDcos30°=
,GB=ABsin60°=
,(6分)
所以G(0,0,0),D(0,1,0),P(0,0,
),C(
,2,0),
=(0,1,-
),
=(
,2,-
)(7分)
设平面PCD的法向量为
=(x,y,z),
∴
,即
令z=1,则x=-1,y=
,∴
=(-1,
,1),(8分)
又平面PBG的法向量为
=(0,2,0),(9分)
设平面PBG与平面PCD所成二面角的平面角为θ,则
∴cosθ =
=
=
即平面PBG与平面PCD所成二面角的平面角的余弦值为
.(10分)
(3)当F为PC的中点时,平面DEF⊥平面ABCD.(11分)
取PC的中点F,连结DE,EF,DF,CG,且DE与CG相交于H.
因为E、G分别为BC、AD的中点,
∴四边形CDGE为平行四边形,
∴H为CG的中点.又F为CP的中点,∴FH∥PG.(12分)
由(2),得PG⊥平面ABCD,∴FH⊥平面ABCD.(13分)
又FH?平面DEF,∴平面DEF⊥平面ABCD.(14分)
(1)证明:连结BD.
因为ABCD为棱形,且∠DAB=60°,

所以△ABD为正三角形.(1分)
又G为AD的中点,所以BG⊥AD.(2分)
又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,(3分)
∴BG⊥平面PAD.(4分)
(2)解:∵△PAD为正三角形,G为AD的中点,∴PG⊥AD.
∵PG?平面PAD,由(1)得:PG⊥GB.又由(1)知BG⊥AD.
∴PG、BG、AD两两垂直.(5分)
故以G为原点,建立如图所示空间直角坐标系G-xyz,
PG=PDcos30°=
| 3 |
| 3 |
所以G(0,0,0),D(0,1,0),P(0,0,
| 3 |
| 3 |
| PD |
| 3 |
| PC |
| 3 |
| 3 |
设平面PCD的法向量为
| n |
∴
|
|
令z=1,则x=-1,y=
| 3 |
| n |
| 3 |
又平面PBG的法向量为
| AD |
设平面PBG与平面PCD所成二面角的平面角为θ,则
∴cosθ =
| ||||
|
|
2
| ||
2
|
| ||
| 5 |
即平面PBG与平面PCD所成二面角的平面角的余弦值为
| ||
| 5 |
(3)当F为PC的中点时,平面DEF⊥平面ABCD.(11分)
取PC的中点F,连结DE,EF,DF,CG,且DE与CG相交于H.
因为E、G分别为BC、AD的中点,
∴四边形CDGE为平行四边形,
∴H为CG的中点.又F为CP的中点,∴FH∥PG.(12分)
由(2),得PG⊥平面ABCD,∴FH⊥平面ABCD.(13分)
又FH?平面DEF,∴平面DEF⊥平面ABCD.(14分)
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,考查平面与平面垂直的证明,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
若点P(x,y)在椭圆
+
=1上,则x的范围是( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、[-4,4] | ||||
| B、[-2,2] | ||||
| C、[-3,3] | ||||
D、[-
|

 如图,椭圆C:
如图,椭圆C: A,B是焦点为F的抛物线y2=4x上的两动点,线段AB的中点M在直线x=t(t>0)上.
A,B是焦点为F的抛物线y2=4x上的两动点,线段AB的中点M在直线x=t(t>0)上.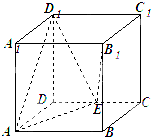 正方体ABCD-A1B1C1D1中,点E在棱CD上.
正方体ABCD-A1B1C1D1中,点E在棱CD上.