题目内容
13.不等式组$\left\{{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}}\right.$表示的平面区域的面积是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 画出不等式组$\left\{{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}}\right.$表示的平面区域为直角三角形ABC及其内部的部分,求得A、B、C各个点的坐标,可得直角三角形ABC的面积.
解答  解:不等式组$\left\{{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}}\right.$表示的平面区域为直角三角形ABC及其内部的部分,如图所示:容易求得A(0,1),
解:不等式组$\left\{{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}}\right.$表示的平面区域为直角三角形ABC及其内部的部分,如图所示:容易求得A(0,1),
C(2,0),B(2,1),
不等式组$\left\{{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}}\right.$表示的平面区域的面积是直角三角形ABC的面积,即 $\frac{1}{2}$×AB×BC=$\frac{1}{2}$×2×1=1,
故选:A.
点评 本题主要考查二元一次不等式组表示平面区域,体现了数形结合的数学思想,属于基础题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
3.某中学为了解高中入学新生的身高情况,从高一年级学生中按分层抽样共抽取了50名学生的身高数据,分组统计后得到了这50名学生身高的频数分布表:
(Ⅰ)在答题卡上作出这50名学生身高的频率分布直方图;
(Ⅱ)估计这50名学生身高的方差(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从身高在[175,185]这6名学生中随机抽取3名,求至少抽到1名女生的概率.
| 身高(cm)分组 | [145,155) | [155,165) | [165,175) | [175,185] |
| 男生频数 | 1 | 5 | 12 | 4 |
| 女生频数 | 7 | 15 | 4 | 2 |
(Ⅱ)估计这50名学生身高的方差(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从身高在[175,185]这6名学生中随机抽取3名,求至少抽到1名女生的概率.
1.已知sinα-cosα=$\frac{1}{3}$,则cos($\frac{π}{2}$-2α)=( )
| A. | -$\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{8}{9}$ | D. | $\frac{\sqrt{17}}{9}$ |
8.命题“?x∈N,x2>x”的否定为( )
| A. | ?x∈N,x2≤x | B. | ?x0∈N,${x}_{0}^{2}$≤x0 | C. | ?x∉N,x2>x | D. | ?x0∉N,${x}_{0}^{2}$≤x0 |
5.某产品的广告费用x万元与销售额y万元的统计数据如表:
根据上表可得回归方程$\widehaty=9.4x+a$,据此模型预测,广告费用为6万元时的销售额为( )万元.
| 广告费用x | 2 | 3 | 4 | 5 |
| 销售额y | 26 | 39 | 49 | 54 |
| A. | 65.5 | B. | 66.6 | C. | 67.7 | D. | 72 |
2.已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且当PA与抛物线相切时,点P恰好在以A、B为焦点的双曲线上,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{2}+1}}{2}$ | C. | $\sqrt{2}+1$ | D. | $\sqrt{5}-1$ |
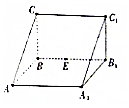 如图,直三棱柱ABC-A1B1C1中,AA1=2,AB=BC=1,∠ABC=90°,外接球的球心为O,点E是侧棱BB1上的一个动点.有下列判断:
如图,直三棱柱ABC-A1B1C1中,AA1=2,AB=BC=1,∠ABC=90°,外接球的球心为O,点E是侧棱BB1上的一个动点.有下列判断: