题目内容
1.已知sinα-cosα=$\frac{1}{3}$,则cos($\frac{π}{2}$-2α)=( )| A. | -$\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{8}{9}$ | D. | $\frac{\sqrt{17}}{9}$ |
分析 由已知,利用二倍角公式可求sin2α的值,进而利用诱导公式即可化简求值得解.
解答 解:∵sinα-cosα=$\frac{1}{3}$,
∴两边平方,可得:1-2sinαcosα=$\frac{1}{9}$,可得:1-sin2α=$\frac{1}{9}$,
∴cos($\frac{π}{2}$-2α)=sin2α=$\frac{8}{9}$.
故选:C.
点评 本题主要考查了二倍角公式,诱导公式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.设集合A1={a1},A2={a2,a3},A3={a4,a5,a6},A4={a7,a8,a9,a10},…,其中{an}为公差大于0的等差数列,若A2={3,5},则199属于( )
| A. | A12 | B. | A13 | C. | A14 | D. | A15 |
9.已知A(2,0),直线4x+3y+1=0被圆C:(x+3)2+(y-m)2=13(m<3)所截得的弦长为4$\sqrt{3}$,且P为圆C上任意一点,则|PA|的最大值为( )
| A. | $\sqrt{29}$-$\sqrt{13}$ | B. | 5+$\sqrt{13}$ | C. | 2$\sqrt{7}$+$\sqrt{13}$ | D. | $\sqrt{29}$+$\sqrt{13}$ |
16.已知一只蚂蚁在边长分别为5,12,13的三角形的边上随机爬行,则其恰在离三个顶点的距离都大于1的地方的概率为( )
| A. | $\frac{π}{60}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{π}{3}$ |
6.已知一长方体的体对角线的长为l0,这条对角线在长方体一个面上的正投影长为8,则这个长方体体积的最大值为( )
| A. | 64 | B. | 128 | C. | 192 | D. | 384 |
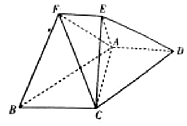 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.