题目内容
2.已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且当PA与抛物线相切时,点P恰好在以A、B为焦点的双曲线上,则双曲线的离心率为( )| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{2}+1}}{2}$ | C. | $\sqrt{2}+1$ | D. | $\sqrt{5}-1$ |
分析 设直线AP的方程,代入抛物线方程,由△=0,求得切线方程,求得P点坐标,根据双曲线的定义,即可求得a的值,c=1,根据双曲线的离心率公式即可求得双曲线的离心率.
解答 解:过P作准线的垂线,垂足为N,由直线PA与抛物线相切,
设直线AP的方程为y=kx-1,
$\left\{\begin{array}{l}{y=kx-1}\\{{y}^{2}=4y}\end{array}\right.$,整理得:x2-4kx+4=0,
∴△=16k2-16=0,
∴k=±1,
∴P(2,1),
∴双曲线的实轴长为丨PA丨-丨PB丨=2($\sqrt{2}$-1),则a=$\sqrt{2}$-1,c=1,
∴双曲线的离心率为e=$\frac{c}{a}$=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1,
则双曲线的离心率$\sqrt{2}$+1,
故选C.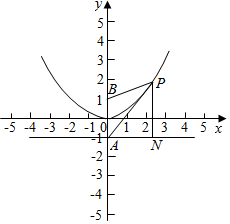
点评 本题考查直线与抛物线的位置关系,考查双曲线的离心率,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
12.设集合A1={a1},A2={a2,a3},A3={a4,a5,a6},A4={a7,a8,a9,a10},…,其中{an}为公差大于0的等差数列,若A2={3,5},则199属于( )
| A. | A12 | B. | A13 | C. | A14 | D. | A15 |
13.不等式组$\left\{{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}}\right.$表示的平面区域的面积是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\frac{\sqrt{2}+1}{2}$ | D. | $\sqrt{2}$+1 |
7.已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=5,则球O的表面积为( )
| A. | 50π | B. | 100π | C. | 200π | D. | $\frac{{125\sqrt{2}π}}{3}$ |
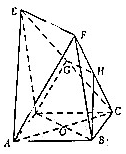 如图,在多面体ABCDEF中,底面ABCD是边长为1的正方形,四边形BDEF是矩形,且BF=2,CF=$\sqrt{5}$,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为1的正方形,四边形BDEF是矩形,且BF=2,CF=$\sqrt{5}$,G和H分别是CE和CF的中点.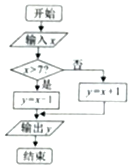 已知实数x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.
已知实数x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.