题目内容
18．
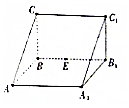如图，直三棱柱ABC-A1B1C1中，AA1=2，AB=BC=1，∠ABC=90°，外接球的球心为O，点E是侧棱BB1上的一个动点．有下列判断：①直线AC与直线C1E是异面直线；
②A1E一定不垂直AC1；
③三棱锥E-AA1O的体积为定值；
④AE+EC1的最小值为$2\sqrt{2}$．
其中正确的个数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 由题意画出图形，由异面直线的概念判断①；利用线面垂直的判定与性质判断②；找出球心，由棱锥底面积与高为定值判断③；设BE=x，列出AE+EC1关于x的函数式，结合其几何意义求出最小值判断④．
解答 解：如图，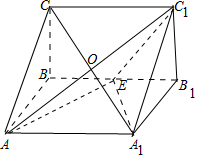
∵直线AC经过平面BCC1B1内的点C，而直线C1E在平面BCC1B1内不过C，∴直线AC与直线C1E是异面直线，故①正确；
当E与B重合时，AB1⊥A1B，而C1B1⊥A1B，∴A1B⊥平面AB1C1，则A1E垂直AC1，故②错误；
由题意知，直三棱柱ABC-A1B1C1的外接球的球心为O是AC1 与A1C 的交点，则△AA1O的面积为定值，由BB1∥平面AA1C1C，
∴E到平面AA1O的距离为定值，∴三棱锥E-AA1O的体积为定值，故③正确；
设BE=x，则B1E=2-x，∴AE+EC1=$\sqrt{1+{x}^{2}}+\sqrt{1+（2-x）^{2}}$．由其几何意义，即平面内动点（x，1）与两定点（0，0），（2，0）距离和的最小值知，其最小值为$2\sqrt{2}$，故④正确．
∴正确命题的个数是3个．
故选：C．
点评 本题考查命题的真假判断与应用，考查空间想象能力和思维能力，属中档题．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
8．若椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的短轴长等于焦距，则椭圆的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{2}}}{4}$ |
9．已知A（2，0），直线4x+3y+1=0被圆C：（x+3）2+（y-m）2=13（m＜3）所截得的弦长为4$\sqrt{3}$，且P为圆C上任意一点，则|PA|的最大值为（ ）
| A． | $\sqrt{29}$-$\sqrt{13}$ | B． | 5+$\sqrt{13}$ | C． | 2$\sqrt{7}$+$\sqrt{13}$ | D． | $\sqrt{29}$+$\sqrt{13}$ |
6．已知一长方体的体对角线的长为l0，这条对角线在长方体一个面上的正投影长为8，则这个长方体体积的最大值为（ ）
| A． | 64 | B． | 128 | C． | 192 | D． | 384 |
13．不等式组$\left\{{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}}\right.$表示的平面区域的面积是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
3．已知函数$f（x）=\frac{x^3}{cosx}$的定义域为$（{-\frac{π}{2}，\frac{π}{2}}）$，当$|{x_i}|＜\frac{π}{2}$（i=1，2，3）时，若x1+x2＞0，x2+x3＞0，x1+x3＞0，则有f（x1）+f（x2）+f（x3）的值（ ）
| A． | 恒小于零 | B． | 恒等于零 | ||
| C． | 恒大于零 | D． | 可能大于零，也可能小于零 |
7．已知三棱柱ABC-A1B1C1的6个顶点都在球O的球面上，若AB=3，AC=4，AB⊥AC，AA1=5，则球O的表面积为（ ）
| A． | 50π | B． | 100π | C． | 200π | D． | $\frac{{125\sqrt{2}π}}{3}$ |
16．若集合A={-2，0，2，3}，B={-1，0，1，2}，则A∩B=（ ）
| A． | {0，1} | B． | {0，2} | C． | {1，3} | D． | {2，3} |