题目内容
11.函数y=x+cosx在区间$[{0,\frac{π}{2}}]$上的最大值是$\frac{π}{2}$.分析 求导,根据导数与函数单调性及最值的关系,即可求得函数y=x+cosx在区间$[{0,\frac{π}{2}}]$上的最大值.
解答 解:由函数y=x+cosx,y′=1-sinx,
令y′=0,而x∈$[{0,\frac{π}{2}}]$,则x=$\frac{π}{2}$,
当x∈$[{0,\frac{π}{2}}]$时,y′≥0,
则y=x+cosx在$[{0,\frac{π}{2}}]$单调递增,
则当x=$\frac{π}{2}$时,y=x+cosx取最大值,
最大值为$\frac{π}{2}$,
函数y=x+cosx在区间$[{0,\frac{π}{2}}]$上的最大值$\frac{π}{2}$,
故答案为:$\frac{π}{2}$.
点评 本题考查导数的综合应用,考查导数与函数单调性及最值的关系,考查计算能力,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
13.不等式组$\left\{{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}}\right.$表示的平面区域的面积是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.若集合A={-2,0,2,3},B={-1,0,1,2},则A∩B=( )
| A. | {0,1} | B. | {0,2} | C. | {1,3} | D. | {2,3} |
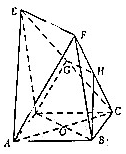 如图,在多面体ABCDEF中,底面ABCD是边长为1的正方形,四边形BDEF是矩形,且BF=2,CF=$\sqrt{5}$,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为1的正方形,四边形BDEF是矩形,且BF=2,CF=$\sqrt{5}$,G和H分别是CE和CF的中点.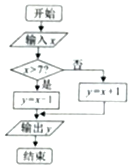 已知实数x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.
已知实数x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.