题目内容
4.P为双曲线x2$-\frac{{y}^{2}}{3}$=1右支上一点,F1,F2为左、右焦点,若|PF1|+|PF2|=10,则$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=18.分析 设P点坐标,根据向量数量积的坐标运算,及两点之间距离公式,由P在椭圆上,即可求得P点坐标,即可求得答案.
解答 解:设P(x,y),由F1,F2分别为左、右焦点,即F1(-2,0),F2(2,0),
∴$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=(-2-x,y)(2-x,y)=-(4-x2)+y2=-4+x2+y2,
由P在双曲线x2$-\frac{{y}^{2}}{3}$=1,即3x2-y2=3,
∴$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=-4+x2+y2=4x2-7,
设丨$\overrightarrow{P{F}_{1}}$丨=$\sqrt{(-2-x)^{2}+{y}^{2}}$,丨$\overrightarrow{P{F}_{2}}$丨=$\sqrt{(2-x)^{2}+{y}^{2}}$,
则丨$\overrightarrow{P{F}_{1}}$丨+丨$\overrightarrow{P{F}_{2}}$丨=$\sqrt{(2+x)^{2}+{y}^{2}}$+=$\sqrt{(2-x)^{2}+{y}^{2}}$=10,
将3x2-y2=3,代入上式,
解得x=$\frac{5}{2}$,
故$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=-4+x2+y2=4x2-7=25-7=18,
故答案为:18,
点评 本题考查向量数量积的坐标运算,两点之间的距离公式,考查计算能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
14. 一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产的零件中有缺点的零件数随机器运转的速度而变化,如表为抽样数据:
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产的零件中有缺点的零件数随机器运转的速度而变化,如表为抽样数据:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)根据散点图判断,y=ax+b与$y=c\sqrt{x}+d$哪一个适宜作为每小时生产的零件中有缺点的零件数y关于转速x的回归方程类型 (给出判断即可,不必说明理由),根据判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)若实际生产中,允许每小时生产的零件中有缺点的零件数最多为10个,那么机器的运转速度应控制在什么范围内?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.)
 一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产的零件中有缺点的零件数随机器运转的速度而变化,如表为抽样数据:
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产的零件中有缺点的零件数随机器运转的速度而变化,如表为抽样数据:| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
(Ⅱ)根据散点图判断,y=ax+b与$y=c\sqrt{x}+d$哪一个适宜作为每小时生产的零件中有缺点的零件数y关于转速x的回归方程类型 (给出判断即可,不必说明理由),根据判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)若实际生产中,允许每小时生产的零件中有缺点的零件数最多为10个,那么机器的运转速度应控制在什么范围内?
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.)
12.设集合A1={a1},A2={a2,a3},A3={a4,a5,a6},A4={a7,a8,a9,a10},…,其中{an}为公差大于0的等差数列,若A2={3,5},则199属于( )
| A. | A12 | B. | A13 | C. | A14 | D. | A15 |
19.若集合M={x|x2+5x-14<0},N={x|m<x<m+3},且M∩N=∅,则m的取值范围为( )
| A. | (-10,2) | B. | (-∞,-10)∪(2,+∞) | C. | [-10,2] | D. | (-∞,-10]∪[2,+∞) |
9.已知A(2,0),直线4x+3y+1=0被圆C:(x+3)2+(y-m)2=13(m<3)所截得的弦长为4$\sqrt{3}$,且P为圆C上任意一点,则|PA|的最大值为( )
| A. | $\sqrt{29}$-$\sqrt{13}$ | B. | 5+$\sqrt{13}$ | C. | 2$\sqrt{7}$+$\sqrt{13}$ | D. | $\sqrt{29}$+$\sqrt{13}$ |
16.已知一只蚂蚁在边长分别为5,12,13的三角形的边上随机爬行,则其恰在离三个顶点的距离都大于1的地方的概率为( )
| A. | $\frac{π}{60}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{π}{3}$ |
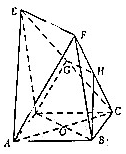 如图,在多面体ABCDEF中,底面ABCD是边长为1的正方形,四边形BDEF是矩形,且BF=2,CF=$\sqrt{5}$,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为1的正方形,四边形BDEF是矩形,且BF=2,CF=$\sqrt{5}$,G和H分别是CE和CF的中点.