题目内容
函数y=a2x+2ax-1(a>0且a≠1)在[-1,1]上有最大值14.
(1)求a的值;
(2)若a,b,c为不等于1的正数,ax=by=cz,且
+
+
=0,求abc的值.
(1)求a的值;
(2)若a,b,c为不等于1的正数,ax=by=cz,且
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
考点:指数函数综合题
专题:综合题,函数的性质及应用
分析:(1)令b=ax构造二次函数y=b2+2b-1,然后根据a的不同范围(a>1或0<a<1)确定b的范围后可解;
(2)令ax=by=cz=m,则x=logam,y=logbm,z=logcm,代入
+
+
=0,利用对数运算法则可求;
(2)令ax=by=cz=m,则x=logam,y=logbm,z=logcm,代入
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
解答:
解:(1)令t=ax,则a2x=t2,
∴y=t2+2t-1=(t+1)2-2,对称轴t=-1,
若0<a<1,则t=ax是减函数,∴a-1>a,
∴0<a<t<
,
∴y的图象都在对称轴t=-1的右边,开口向上 并且递增,
∴t=
时有最大值,
∴y=t2+2t-1=14,∴t2+2t-15=0,∴(t-3)(t+5)=0,
∵t>0,∴t=
=3,a=
符合0<a<1;
若a>1则t=ax是增函数,此时0<
<t<a,
y的图象仍在对称轴b=-1的右边,∴还是增函数,t=a时有最大值,
∴y=t2+2t-1=14,
t>0,∴t=a=3,符合a>1;
综上,a=
或a=3;
(2)令ax=by=cz=m,则x=logam,y=logbm,z=logcm,
∴
+
+
=0,即为logma+logmb+logmc=0,
∴logmabc=0,∴abc=1.
∴y=t2+2t-1=(t+1)2-2,对称轴t=-1,
若0<a<1,则t=ax是减函数,∴a-1>a,
∴0<a<t<
| 1 |
| a |
∴y的图象都在对称轴t=-1的右边,开口向上 并且递增,
∴t=
| 1 |
| a |
∴y=t2+2t-1=14,∴t2+2t-15=0,∴(t-3)(t+5)=0,
∵t>0,∴t=
| 1 |
| a |
| 1 |
| 3 |
若a>1则t=ax是增函数,此时0<
| 1 |
| a |
y的图象仍在对称轴b=-1的右边,∴还是增函数,t=a时有最大值,
∴y=t2+2t-1=14,
t>0,∴t=a=3,符合a>1;
综上,a=
| 1 |
| 3 |
(2)令ax=by=cz=m,则x=logam,y=logbm,z=logcm,
∴
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
∴logmabc=0,∴abc=1.
点评:本题主要考查指数函数单调性、对数运算法则及其应用,考查分类讨论思想.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知a>b>0,c>d>0,下列判断中正确的是( )
| A、a-c<b-d | ||||
| B、ac>bd | ||||
C、
| ||||
| D、ad>bc |
已知
=21,则(2
-
)n的二项展开式中的常数项为( )
| C | n-1 n+1 |
| x |
| 1 | ||
|
| A、160 | B、-160 |
| C、960 | D、-960 |
Sn是数列{an}的前n项和,an=
,则S1=1-
,S2=1-
,S3=1-
,S4=1-
,由此可以归纳出( )
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
A、Sn=1-
| ||
B、Sn=1-
| ||
C、Sn=1-
| ||
D、Sn=1-
|
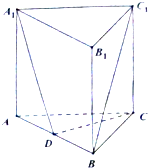 如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1.
如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1.