题目内容
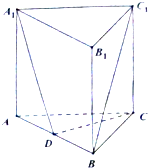 如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1.
如图,在三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1=2,D为AB的中点,且CD⊥DA1.(1)求证:BB1⊥平面ABC.
(2)求证:BC1∥平面CA1D.
(3)求三棱锥C-A1BD的体积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)先证明出CD⊥AB,进而证明出CD⊥DA1,DA1则可利用线面垂直的判定定理证明出CD⊥平面ABB1A1,进而可知BB1⊥CD,最后根据线面垂直的判定定理证明出BB1⊥平面ABC.
(2)先证明出BC1∥DE,继而根据线面平行的判定定理证明出BC1∥平面CA1D.
(3)先判断出CD是三棱锥的高,进而根据三棱锥的体积公式求得答案.
(2)先证明出BC1∥DE,继而根据线面平行的判定定理证明出BC1∥平面CA1D.
(3)先判断出CD是三棱锥的高,进而根据三棱锥的体积公式求得答案.
解答:
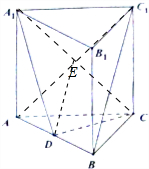 证明:(1)∵AC=BC,D为AB的中点,
证明:(1)∵AC=BC,D为AB的中点,
∴CD⊥AB,
∵CD⊥DA1,DA1∩AB=D,
∴CD⊥平面ABB1A1,
∵BB1⊥CD,BB1⊥AB,
∴BB1⊥平面ABC.
(2)连接AC1交A1C与E,连接DE,则BC1∥DE,
∵DE?平面CA1D,BC1?平面CA1D,
∴BC1∥平面CA1D.
(3)∵CD⊥ABB1A1,
∴CD是三棱锥的高,
在Rt△ABC中,AC=BC=2,
∴AB=2
,CD=
,
∴VC-A1BD=
S•CD=
×
×2×
=
.
 证明:(1)∵AC=BC,D为AB的中点,
证明:(1)∵AC=BC,D为AB的中点,∴CD⊥AB,
∵CD⊥DA1,DA1∩AB=D,
∴CD⊥平面ABB1A1,
∵BB1⊥CD,BB1⊥AB,
∴BB1⊥平面ABC.
(2)连接AC1交A1C与E,连接DE,则BC1∥DE,
∵DE?平面CA1D,BC1?平面CA1D,
∴BC1∥平面CA1D.
(3)∵CD⊥ABB1A1,
∴CD是三棱锥的高,
在Rt△ABC中,AC=BC=2,
∴AB=2
| 2 |
| 2 |
∴VC-A1BD=
| 1 |
| 3 |
| 1 |
| 6 |
| 2 |
| 2 |
| 2 |
| 3 |
点评:本题主要考查了线面平行和线面垂直的判定定理的应用,三棱锥体积的计算.考查了学生立体几何 综合素质.

练习册系列答案
相关题目
已知x、y满足约束条件
,则目标函数z=2x+y( )
|
| A、最大值为1 |
| B、最大值为2 |
| C、最大值为3 |
| D、以上都不对 |
cos660°的值为( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
用数学归纳法证明12+32+52+…+(2n-1)2=
n(4n2-1)过程中,由n=k递推到n=k+1时,不等式左边增加的项为( )
| 1 |
| 3 |
| A、(2k)2 |
| B、(2k+3)2 |
| C、(2k+2)2 |
| D、(2k+1)2 |
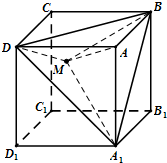 如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若f(M)=(
如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若f(M)=(  已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为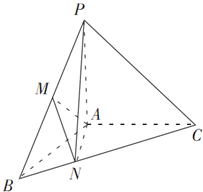 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且AN=
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP,M为PB的中点,N在BC上,且AN=