题目内容
若一个圆的圆心在直线y=2x上,在y轴上截得的弦的长度等于2,且与直线x-y+
=0相切,则这个圆的方程可能是( )
| 2 |
| A、x2+y2-x-2y=0 |
| B、x2+y2+2x+4y=0 |
| C、x2+y2-2=0 |
| D、x2+y2-1=0 |
考点:圆的切线方程
专题:直线与圆
分析:本题先用待定系数法设出圆的标准方程,再利用圆心在直线上,得到一个关系式,用圆与直线相切得到一个关系式,再通过弦长和勾股定理得到一个关系式,解关系式组求出参数,得到圆的方程.
解答:
解:由于圆心在直线y=2x上所以可以设圆心的坐标为(a,2a)
设圆的半径为r,
∵圆与直线x-y+
=0相切,
∴圆心(a,2a)到直线的距离
=r,①.
又因为圆y轴截得的弦长为2,半弦长为1,
所以a2+1=r2将其带入①式得
=a2+1,
解得a=0或a=-2
.
∴圆的标准方程为x2+y2=1或(x+2
)2+(y+4
)2=9,
故选:D.
设圆的半径为r,
∵圆与直线x-y+
| 2 |
∴圆心(a,2a)到直线的距离
|a-2a+
| ||
|
又因为圆y轴截得的弦长为2,半弦长为1,
所以a2+1=r2将其带入①式得
(
| ||
| 2 |
解得a=0或a=-2
| 2 |
∴圆的标准方程为x2+y2=1或(x+2
| 2 |
| 2 |
故选:D.
点评:本题考查了圆的方程知识和函数方程思想,本题思维难度不大,但有一定的计算量,属于中档题.

练习册系列答案
相关题目
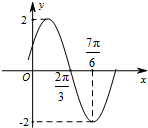 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<| π |
| 2 |
A、f(x)=2sin(2x+
| ||
B、f(x)=2sin(x+
| ||
C、f(x)=2sin(2x+
| ||
D、f(x)=2sin(x+
|
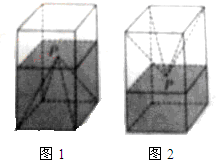 如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P,如果将容器倒置,水面也恰好过点P(如图2),有下列三个命题:
如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P,如果将容器倒置,水面也恰好过点P(如图2),有下列三个命题: