题目内容

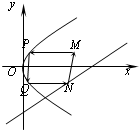如图，从点M（x0，4）发出的光线，沿平行于抛物线y2=8x的对称轴方向射向此抛物线上的点P，经抛物线反射后，穿过焦点射向抛物线上的点Q，再经抛物线反射后射向直线l：x-y-10=0上的点N，经直线反射后又回到点M，则x0等于（　　）
A、5B、6C、7D、8
考点：抛物线的简单性质
专题：综合题,圆锥曲线的定义、性质与方程
分析：由题意可得抛物线的轴为x轴，抛物线的焦点F（1，0），MP所在的直线方程为y=4，从而可求P（2，4），Q（2，-4），N（6，-4），确定直线MN的方程，可求答案．
解答： 解：由题意可得抛物线的轴为x轴，F（2，0），
∴MP所在的直线方程为y=4
在抛物线方程y2=8x中，
令y=4可得x=2，即P（2，4）
从而可得Q（2，-4），N（6，-4）
∵经抛物线反射后射向直线l：x-y-10=0上的点N，经直线反射后又回到点M，
∴直线MN的方程为x=6
故选：B．
点评：本题主要考查了抛物线的性质的应用，解决问题的关键是要熟练掌握相关的性质并能灵活应用．
练习册系列答案
相关题目
下列四个命题中正确的命题序号是（　　）
①向量
a
，
b
共线的充分必要条件是存在唯一实数λ，使
a
=λ
b
成立．
②函数y=f（x-1）与y=f（1-x）的图象关于直线x=1对称．
③ysinθ-cosθ=2y（θ∈[0，π]）成立的充分必要条件是|2y|≤
1+y2
．
④已知U为全集，则x∉A∩B的充分条件是x∈（∁UA）∩（∁UB）．
A、②④B、①②C、①③D、③④
下列说法：
（1）命题“?x∈R，2x≤0”的否定是“?x∈R，2x＞0”；
（2）关于x的不等式a＜sin2x+
2
sin2x
恒成立，则a的取值范围是a＜3；
（3）对于函数f(x)=
ax
1+|x|
(a∈R且a≠0)，则有当a=1时，?k∈（1，+∞），使得函数g（x）=f（x）-kx在R上有三个零点；
（4）
∫
1
0
1-x2
dx≤
∫
e
1
1
x
dx；
（5）已知m，n，s，t∈R+，m+2n=5，
m
s
+
n
t
=9，n＞m，且m，n是常数，又s+2t的最小值是1，则m+3n=7．
其中正确的个数是
 
．
已知集合M={x|x＜1}，集合N={y|y＞0}，则M∩N=（　　）
A、{x|x＜1}
B、{x|x＞1}
C、{x|0＜x＜1}
D、∅
若实数x，y满足不等式组
3x-y≤3
x+y≥1
x-y≥-1
，则z=2x+3y的最大值是（　　）
A、13B、12C、11D、10
如果直线3x-
3
y+m=0与双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）恒有两个公共点，则双曲线C的离心率的取值范围是（　　）
A、（1，2）
B、（2，+∞）
C、（1，2]
D、[2，+∞）
如图所示的程序框图，能使输入的x值与输出的y值相等的x值个数为（　　）
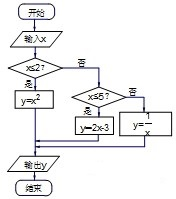
A、1B、2C、3D、4
已知过点P（2，-1）的直线l交椭圆
x 2
8
+
y 2
4
=1于M、N两点，B（0，2）是椭圆的一个顶点，若线段MN的中点恰为点P．
（Ⅰ）求直线l的方程；
（Ⅱ）求△BMN的面积．
在平面直角坐标系xOy中，已知圆C1：（x+1）2+y2=1，圆C2：（x-3）2+（y-4）2=1．
（Ⅰ）若过点C1（-1，0）的直线l被圆C2截得的弦长为
6
5
，求直线l的方程；
（Ⅱ）圆D是以1为半径，圆心在圆C3：（x+1）2+y2=9上移动的动圆，若圆D上任意一点P分别作圆C1的两条切线PE，PF，切点为E，F，求
C1E
•
C1F
的取值范围；
（Ⅲ）若动圆C同时平分圆C1的周长、圆C2的周长，则动圆C是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网