题目内容
已知双曲线C: 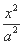 -
-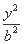 =1的焦距为10,点P(2,1)在C的渐近线上,则C的方程
=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程
为( )
(A)  -
-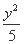 =1 (B)
=1 (B)  -
-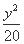 =1
=1
(C)  -
-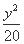 =1 (D)
=1 (D)  -
- =1
=1
A

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
题目内容
已知双曲线C: 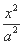 -
-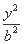 =1的焦距为10,点P(2,1)在C的渐近线上,则C的方程
=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程
为( )
(A)  -
-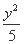 =1 (B)
=1 (B)  -
-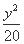 =1
=1
(C)  -
-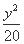 =1 (D)
=1 (D)  -
- =1
=1
A

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案