题目内容
已知函数f(x)=x|x-a|(a∈R).
(Ⅰ)当a=2时,在给定的平面直角坐标系中作出f(x)的图象,并写出f(x)的单调区间;
(Ⅱ)当a=-2时,求函数y=f(x)在区间(-
-1,2]上的值域.
(Ⅰ)当a=2时,在给定的平面直角坐标系中作出f(x)的图象,并写出f(x)的单调区间;
(Ⅱ)当a=-2时,求函数y=f(x)在区间(-
| 2 |

考点:函数的图象,函数的值域
专题:计算题,作图题,函数的性质及应用
分析:(Ⅰ)当a=2时,f(x)=x|x-2|,作出f(x)的图象,由图象写出f(x)的单调区间;
(Ⅱ)当a=-2时,f(x)=x|x+2|=
,从而分别求f(x)的取值范围,从而求函数的值域.
(Ⅱ)当a=-2时,f(x)=x|x+2|=
|
解答:
解:(Ⅰ)当a=2时,f(x)=x|x-2|,
其图象如下:

则f(x)的单调增区间为(-∞,1],[2,+∞);单调减区间[1,2];
(Ⅱ)当a=-2时,
f(x)=x|x+2|=
,
若-2≤x≤2,
则-1≤x2+2x≤8,
若-
-1≤x<-2,则
(-
-1)(
-1)≤f(x)<0,
即-1)≤f(x)<0,
综上所述,函数y=f(x)在区间(-
-1,2]上的值域为[-1,8].
其图象如下:

则f(x)的单调增区间为(-∞,1],[2,+∞);单调减区间[1,2];
(Ⅱ)当a=-2时,
f(x)=x|x+2|=
|
若-2≤x≤2,
则-1≤x2+2x≤8,
若-
| 2 |
(-
| 2 |
| 2 |
即-1)≤f(x)<0,
综上所述,函数y=f(x)在区间(-
| 2 |
点评:本题考查了函数的化简与函数图象的作法,同时考查了分段函数的值域的求法,属于中档题.

练习册系列答案
相关题目
若数列{an}是等比数列,a2=1,其前n项和为Sn,则S3的取值范围是( )
| A、(-∞,1] |
| B、(-∞,0)∪(1,+∞) |
| C、[3,+∞) |
| D、(-∞,-1]∪[3,+∞) |
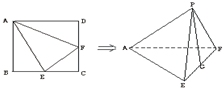 已知正方形ABCD的边长为2,点E、F分别为边BC,CD的中点,沿AE、EF、AF折叠成一个三棱锥P-AEF(使B,C,D重合于点P),则三棱锥P-AEF的外接球的表面积为( )
已知正方形ABCD的边长为2,点E、F分别为边BC,CD的中点,沿AE、EF、AF折叠成一个三棱锥P-AEF(使B,C,D重合于点P),则三棱锥P-AEF的外接球的表面积为( )A、8
| ||
| B、36π | ||
| C、12π | ||
| D、6π |
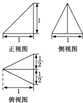
已知某几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1和AB上的点,则下列说法正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1和AB上的点,则下列说法正确的是