题目内容
若数列{an}是等比数列，a2=1，其前n项和为Sn，则S3的取值范围是（ ）
| A、（-∞，1] |
| B、（-∞，0）∪（1，+∞） |
| C、[3，+∞） |
| D、（-∞，-1]∪[3，+∞） |
考点：等比数列的前n项和
专题：等差数列与等比数列,不等式
分析：首先根据等比数列的性质求出a1a3=1，然后对公比q进行分类，利用基本不等式求出结果．
解答：
解：数列{an}是等比数列，a2=1
根据等比数列的性质：a1a3=a22解得：a1a3=1
①当公比q＞0时，S3=a1+a2+a3≥2
+a2=3
②当公比q＜0时，S3=a1+a2+a3≤-2
+a2=-1
则：S3的取值范围：（-∞，-1]∪[3，+∞）
故选：D
根据等比数列的性质：a1a3=a22解得：a1a3=1
①当公比q＞0时，S3=a1+a2+a3≥2
| a1a3 |
②当公比q＜0时，S3=a1+a2+a3≤-2
| a1a3 |
则：S3的取值范围：（-∞，-1]∪[3，+∞）
故选：D
点评：本题考查的知识要点：等比数列的等比中项，基本不等式的应用，分类讨论思想在做题中的应用．
练习册系列答案
相关题目
如图，四边形ABCD是正方形，PD∥MA，MA⊥AD，PM⊥平面CDM，MA=AD=在△ABC中，角A、B、C所对的边分别为a、b、c，若a•cosA=bcosB，则△ABC的形状为（ ）
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰三角形或直角三角形 |
| D、等腰直角三角形 |
已知函数f（x）=x|x-a|（a∈R）．
（Ⅰ）当a=2时，在给定的平面直角坐标系中作出f（x）的图象，并写出f（x）的单调区间；
（Ⅱ）当a=-2时，求函数y=f（x）在区间（-
-1，2]上的值域．
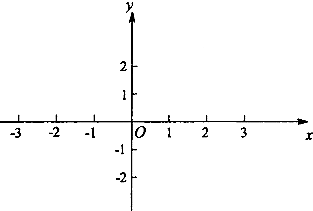
（Ⅰ）当a=2时，在给定的平面直角坐标系中作出f（x）的图象，并写出f（x）的单调区间；
（Ⅱ）当a=-2时，求函数y=f（x）在区间（-
| 2 |
已知圆（x-3）2+（y-4）2=4和直线y=x相交于P，Q两点则|OP|•|OQ|的值是（ ）
A、
| ||
| B、2 | ||
| C、4 | ||
| D、21 |
