题目内容
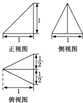
已知某几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由三视图知几何体是一个三棱锥,三棱锥的底面是一个底边是1,高是1的三角形,做出面积三棱锥的高是1,根据三棱锥的体积公式得到结果.
解答:
解:由三视图知几何体是一个三棱锥,
三棱锥的底面是一个底边是1,高是1的三角形,面积是
×1×1=
,
三棱锥的高是1,
∴三棱锥的体积是
×
×1=
cm3,
故选:C.
三棱锥的底面是一个底边是1,高是1的三角形,面积是
| 1 |
| 2 |
| 1 |
| 2 |
三棱锥的高是1,
∴三棱锥的体积是
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故选:C.
点评:本题考查由三视图还原几何体并且看出几何体各个部分的长度,本题解题的关键是要求体积需要求出几何体的底面面积和高.本题是一个基础题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知函数f(x)=x|x-a|(a∈R).
(Ⅰ)当a=2时,在给定的平面直角坐标系中作出f(x)的图象,并写出f(x)的单调区间;
(Ⅱ)当a=-2时,求函数y=f(x)在区间(-
-1,2]上的值域.
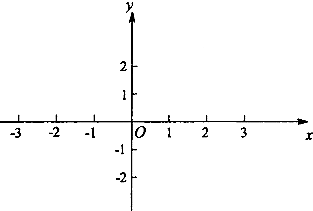
(Ⅰ)当a=2时,在给定的平面直角坐标系中作出f(x)的图象,并写出f(x)的单调区间;
(Ⅱ)当a=-2时,求函数y=f(x)在区间(-
| 2 |

函数f(x)=x3-3x2-9x+3,若函数g(x)=f(x)-m,在x∈[-2,5]上有3个零点,则m的取值范围为( )
| A、[1,8] |
| B、(-24,1] |
| C、[1,8) |
| D、(-24,8) |
如图,在长方形ABCD中,AB=
,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )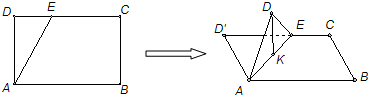
| 3 |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列1,3,6,10…的一个通项公式是( )
| A、an=n2-(n-1) | ||
B、an=
| ||
| C、an=n2-1 | ||
D、an=
|