题目内容
12．
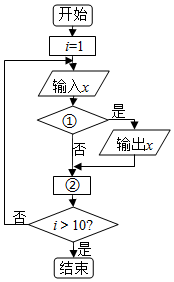如图的程序框图的功能是：给出以下十个数：15，19，80，53，95，73，58，27，60，39，把大于60的数找出来，则框图中的①②应分别填入的是（ ）| A． | x＞60？，i=i+1 | B． | x＜60？，i=i+1 | C． | x＞60？，i=i-1 | D． | x＜60？，i=i-1 |
分析 流程图的功能是把大于60的数找出来，而流程图中可知当满足条件时输出x，故判断框中应填x＞60，处理框用来计数的，从而得到处理框中应填．
解答 解：把大于60的数找出来，根据流程图可知当满足条件时输出x，故判断框中应填x＞60，
处理框用来计数的，则处理框应填i=i+1．
故选：A．
点评 本题主要考查了当型循环结构，循环结构有两种形式：当型循环结构和直到型循环结构，当型循环是先判断后循环，直到型循环是先循环后判断，该题型比较新颖，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
3．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一个焦点到一条渐近线的距离不大于$\frac{{\sqrt{5}}}{3}c$（c为双曲线的半焦距长），则双曲线离心率的取值范围为（ ）
| A． | $[\frac{{3\sqrt{5}}}{2}，+∞）$ | B． | $（1，\frac{3}{2}]$ | C． | $（1，\frac{{3\sqrt{5}}}{2}]$ | D． | $[\frac{3}{2}，+∞）$ |
7．
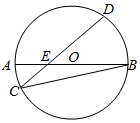如图，圆O的直径AB与弦CD交于点E，且E为OA的中点，若OA=2，∠BCD=30°，则线段CE的长为（ ）
如图，圆O的直径AB与弦CD交于点E，且E为OA的中点，若OA=2，∠BCD=30°，则线段CE的长为（ ）| A． | 1 | B． | $\frac{3\sqrt{5}}{5}$ | C． | $\frac{\sqrt{6}}{2}$ | D． | $\frac{3\sqrt{7}}{7}$ |
17．已知点F是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点，点E是左顶点，过F且垂直于x轴的直线与双曲线交于点A，若tan∠AEF＜1，则双曲线的离心率e的取值范围是（ ）
| A． | （1，+∞） | B． | （1，2） | C． | （1，1+$\sqrt{2}$） | D． | （2，2+$\sqrt{2}$） |
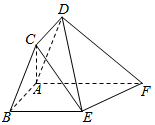如图，在平行四边形ABCD中，AB=1，BC=2，∠CBA=$\frac{π}{3}$，ABEF为直角梯形，BE∥AF，∠BAF=$\frac{π}{2}$，BE=2，AF=3，平面ABCD⊥平面ABEF．