题目内容
2.在平面直角坐标系内有点P(a,b)(a≠b),且a,b∈{1,2,3,4,5,6},当P在圆x2+y2=25内部,求点P的个数.(不要用列举法)分析 分三类,第一类,从{1,2,3]中选2个,第二类,一个从{1,2,3}选,一个选4,第三类,一个选1,一个从{5,6}中选一个,根据分类计数原理可得
解答 解:第一类,从{1,2,3]中选2个,共有3×3=9种,
第二类,一个从{1,2,3}选,一个选4,共有C31A22=6种,
第三类,一个选1,一个从{5,6}中选一个,共有C21A22=4种,
根据分类计数原理,共有9+6+4=19种.
点评 本题考查了点和圆的位置关系以及分类计数原理,属于基础题.

练习册系列答案
相关题目
12.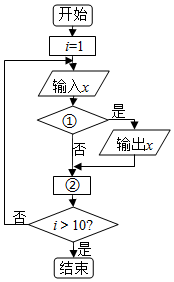 如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
 如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )| A. | x>60?,i=i+1 | B. | x<60?,i=i+1 | C. | x>60?,i=i-1 | D. | x<60?,i=i-1 |
13.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是( )
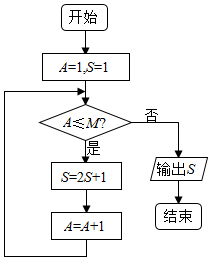

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
10.执行如图所示的程序框图,若输入x=1,则输出y的值是( )
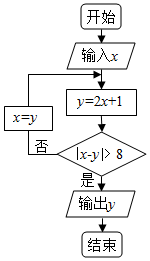

| A. | 7 | B. | 15 | C. | 23 | D. | 31 |
14.某次军事演习要出动一艘航母,2艘攻击型潜艇一前一后,3艘驱逐舰和3艘护卫舰分列左右,每侧3艘,同侧不能都是同种舰艇,则舰艇分配方案的方法数为( )
| A. | 72 | B. | 324 | C. | 648 | D. | 1296 |