题目内容
1.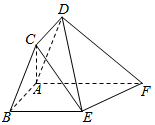 如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.
如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA=$\frac{π}{3}$,ABEF为直角梯形,BE∥AF,∠BAF=$\frac{π}{2}$,BE=2,AF=3,平面ABCD⊥平面ABEF.(1)求证:AC⊥平面ABEF;
(2)求三棱锥D-AEF的体积.
分析 (1)证明AC⊥AB,利用平面ABCD⊥平面ABEF,根据面面垂直的性质定理即可证明AC⊥平面ABEF;
(2)由(1)可知,AC是三棱锥D-AEF的高,利用体积公式求三棱锥D-AEF的体积.
解答 (1)证明:∵AB=1,BC=2,∠CBA=$\frac{π}{3}$,
∴AC2=AB2+BC2-2AB•BCcos$\frac{π}{3}$=1+4-2×2×1×$\frac{1}{2}$=3,
则AC=$\sqrt{3}$,满足BC2=AB2+AC2,
即△CAB是直角三角形,AC⊥AB,
∵平面ABCD⊥平面ABEF,AC?平面ABCD,平面ABCD∩平面ABEF=AB,
∴AC⊥平面ABEF;
(2)解:由(1)可知,AC是三棱锥D-AEF的高,
∵S△AEF=$\frac{1}{2}×3×1$=$\frac{3}{2}$,
∴三棱锥D-AEF的体积V=$\frac{1}{3}×\frac{3}{2}×\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
点评 本题主要考查面面垂直的性质定理,线面垂直的证明,考查三棱锥D-AEF的体积,正确运用面面垂直的性质定理是关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
12.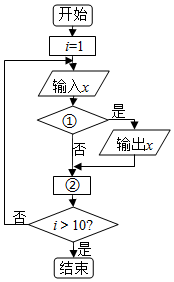 如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
 如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )| A. | x>60?,i=i+1 | B. | x<60?,i=i+1 | C. | x>60?,i=i-1 | D. | x<60?,i=i-1 |
9.等腰直角三角形ABC中,A=90°,A,B在双曲线E的同一支上,且线段AB通过双曲线的一个焦点,C为双曲线E的另一个焦点,则该双曲线的离心率为( )
| A. | $\sqrt{4-2\sqrt{2}}$ | B. | $\sqrt{5-2\sqrt{2}}$ | C. | $\sqrt{4+2\sqrt{2}}$ | D. | $\sqrt{5+2\sqrt{2}}$ |
16.执行如图所示的程序框图,若输出的S值为-4,则条件框内应填写( )


| A. | i>3? | B. | i<5? | C. | i>4? | D. | i<4? |
13.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是( )
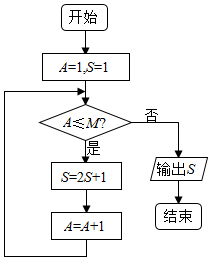

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
10.执行如图所示的程序框图,若输入x=1,则输出y的值是( )
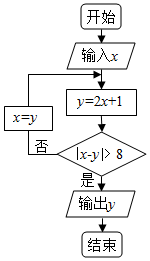

| A. | 7 | B. | 15 | C. | 23 | D. | 31 |