题目内容
17.已知点F是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点,点E是左顶点,过F且垂直于x轴的直线与双曲线交于点A,若tan∠AEF<1,则双曲线的离心率e的取值范围是( )| A. | (1,+∞) | B. | (1,2) | C. | (1,1+$\sqrt{2}$) | D. | (2,2+$\sqrt{2}$) |
分析 由题意可得E(-a,0),F(c,0),|EF|=a+c,令x=c,代入双曲线的方程可得|AF|,再由正切函数的定义,解不等式结合离心率公式,计算即可得到所求范围.
解答 解:由题意可得E(-a,0),F(c,0),
|EF|=a+c,
令x=c,代入双曲线的方程可得y=±b$\sqrt{\frac{{c}^{2}}{{a}^{2}}-1}$=±$\frac{{b}^{2}}{a}$,
在直角三角形AEF中,tan∠AEF=$\frac{|AF|}{|EF|}$=$\frac{\frac{{b}^{2}}{a}}{c+a}$<1,
可得b2<a(c+a),
由b2=c2-a2=(c-a)(c+a),可得
c-a<a,即c<2a,
可得e=$\frac{c}{a}$<2,但e>1,可得1<e<2.
故选:B.
点评 本题考查双曲线的离心率的范围,考查双曲线的方程和性质,注意运用正切函数的定义,考查运算能力,属于中档题.

练习册系列答案
相关题目
12.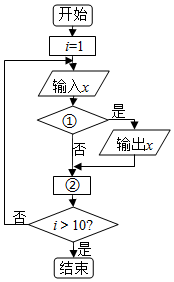 如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
 如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )
如图的程序框图的功能是:给出以下十个数:15,19,80,53,95,73,58,27,60,39,把大于60的数找出来,则框图中的①②应分别填入的是( )| A. | x>60?,i=i+1 | B. | x<60?,i=i+1 | C. | x>60?,i=i-1 | D. | x<60?,i=i-1 |
9.等腰直角三角形ABC中,A=90°,A,B在双曲线E的同一支上,且线段AB通过双曲线的一个焦点,C为双曲线E的另一个焦点,则该双曲线的离心率为( )
| A. | $\sqrt{4-2\sqrt{2}}$ | B. | $\sqrt{5-2\sqrt{2}}$ | C. | $\sqrt{4+2\sqrt{2}}$ | D. | $\sqrt{5+2\sqrt{2}}$ |
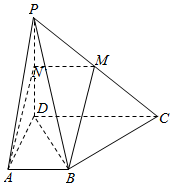 已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,∠DAB=90°,PD⊥底面ABCD,且PD=DA=CD=2AB=2,M为PC的中点,过A,B,M三点的平面与PD交于点N.
已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,∠DAB=90°,PD⊥底面ABCD,且PD=DA=CD=2AB=2,M为PC的中点,过A,B,M三点的平面与PD交于点N.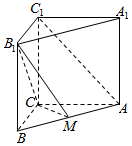 如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点M在线段AB上.
如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点M在线段AB上. 已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点.
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点. 如图所示,四棱锥S-ABCD中,底面ABCD为正方形,且AB=4,SA⊥平面ABCD,∠SDA=60°,E、F、G分别是SC、SD、AC上的点,且$\frac{SE}{EC}$=$\frac{SF}{FD}$=$\frac{AG}{GC}$.
如图所示,四棱锥S-ABCD中,底面ABCD为正方形,且AB=4,SA⊥平面ABCD,∠SDA=60°,E、F、G分别是SC、SD、AC上的点,且$\frac{SE}{EC}$=$\frac{SF}{FD}$=$\frac{AG}{GC}$.