题目内容
已知P为椭圆
+y2=1和双曲线x2-
=1的一个交点,F1,F2为椭圆的焦点,那么
•
= .
| x2 |
| 4 |
| y2 |
| 2 |
| PF1 |
| PF2 |
考点:双曲线的简单性质,椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意,可由椭圆及双曲线的定义得出
+
=4,
-
=2,F1F2=2
,再利用余弦定理解出cos∠F1PF2,再求
•
.
| PF1 |
| PF2 |
| PF1 |
| PF2 |
| 3 |
| PF1 |
| PF2 |
解答:
解:由题意,不妨令点P在y轴的右侧,则有
+
=4,
-
=2
二者联立解得
=3,
=1,又F1F2=2
由余弦定理得cos∠F1PF2=
=-
故
•
=3×1×(-
)=-
.
故答案为-
.
| PF1 |
| PF2 |
| PF1 |
| PF2 |
二者联立解得
| PF1 |
| PF2 |
| 3 |
由余弦定理得cos∠F1PF2=
32+12-(2
| ||
| 2×2×1 |
| 1 |
| 2 |
故
| PF1 |
| PF2 |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为-
| 3 |
| 2 |
点评:本题考查双曲线与椭圆的性质,余弦定理,属于数学基本题,必会题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列六种表示法:①{x=-1,y=2};②{(x,y)|x=-1,y=2|};③{-1,2};④(-1,2);⑤{(-1,2)};⑥{(x,y)|x=-1或y=2}.能表示方程组
的解集的是( )
|
| A、①②③④⑤⑥ | B、②③④⑤ |
| C、②⑤ | D、②⑤⑥ |
已知三棱锥O-ABC,A,B,C三点均在球心为O的球表面上,AB=BC=1,∠ABC=120°,三棱锥O-ABC的体积为
,则球O的表面积是( )
| ||
| 4 |
| A、544π | ||
| B、16π | ||
C、
| ||
| D、64π |
在三棱锥S-ABC中,AB=BC=
,SA=SC=AC=2,二面角S-AC-B的余弦值是
,则三棱锥S-ABC外接球的表面积是( )
| 2 |
| ||
| 3 |
A、
| ||
| B、2π | ||
C、
| ||
| D、6π |
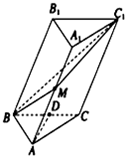 如图所示,在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
如图所示,在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.