题目内容
19.设函数f(x)=$\frac{1}{3}$x3-ax2-3a2x+1(a>0).(Ⅰ)求函数f(x)的单调区间、极大值和极小值.
(Ⅱ)若x∈[a+1,a+2]时,恒有f′(x)>-3a,求实数a的取值范围.
分析 (Ⅰ)判定函数当x变化时,f'(x)的变化情况,f'(x)>0求得单调增区间,f'(x)<0求得单调减区间,f'(x)的变化情况研究出函数的极值;
(Ⅱ)研究x∈[a+1,a+2]时,恒有f'(x)>-3a成立的问题,可转化成f'(x)的最小值大于-3a成立.
解答 解:(Ⅰ)令f'(x)=x2-2ax-3a2=0,得x=-a或x=3a,
则当x变化时,f(x)与f'(x)的变化情况如下表:
| x | (-∞,-a) | -a | (-a,3a) | 3a | (3a,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | $\frac{5}{3}$a3+1 | 递减 | -9a3+1 | 递增 |
当x∈(3a,+∞)时,函数f(x)也为增函数.
当x∈(-a,3a)时,函数f(x)为减函数,
当x=-a时,f(x)的极大值为$\frac{5}{3}$a3+1;
当x=3a时,f(x)的极小值为-9a3+1.
(Ⅱ)因为f'(x)=x2-2ax-3a2的对称轴为x=a,
且其图象的开口向上,
所以f'(x)在区间[a+1,a+2]上是增函数,
则在区间[a+1,a+2]上恒有f'(x)>-3a
等价于f'(x)的最小值大于-3a成立.
所以f'(a+1)=(a+1)2-2a(a+1)-3a2=-4a2+1>-3a,
解得:-$\frac{1}{4}$<a<1:,又a>0,
故a的取值范围是(0,1).
点评 本题考查了利用导数研究函数的单调性、极值以及恒成立问题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
13.定义在R上,且最小正周期为π的函数是( )
| A. | y=sin|x| | B. | y=cos|x| | C. | y=|sinx| | D. | y=|cos2x| |
14.在空间中,下列命题正确的是( )
| A. | 如果平面α⊥平面β,任取直线m?α,那么必有m⊥β | |
| B. | 如果直线m∥平面α,直线n?α内,那么m∥n | |
| C. | 如果直线m∥平面α,直线n∥平面α,那么m∥n | |
| D. | 如果平面α外的一条直线m垂直于平面α内的两条相交直线,那么m⊥α |
14.函数y=lnx-x的单调递减区间是( )
| A. | (1,+∞) | B. | (0,1) | C. | (0,1),(-∞,0) | D. | (1,+∞),(-∞,0) |
11.已知cos($\frac{5π}{12}$-θ)=$\frac{1}{3}$,则sin($\frac{π}{12}$+θ)的值是( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{2\sqrt{2}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
9.一个几何体的三视图如图所示,则该几何体的表面积为( )
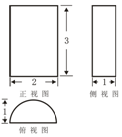

| A. | 4π | B. | 5π+6 | C. | 3π+6 | D. | 4π+6 |
 如图:空间四边形ABCD中,E,F,G,H分别是AB,AD,CD,CB上的点,且EF∥GH,求证:EF∥BD.
如图:空间四边形ABCD中,E,F,G,H分别是AB,AD,CD,CB上的点,且EF∥GH,求证:EF∥BD.