题目内容
函数f(x)=sin(ωx+φ)(-
<φ<
,ω>0)的最小正周期为π,其图象经过点(
,1)
(1)求f(x)的解析式;
(2)若f(a)+f(a-
)=
且a为锐角,求sina+cosa的值.
| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
(1)求f(x)的解析式;
(2)若f(a)+f(a-
| π |
| 3 |
| 24 |
| 25 |
考点:三角函数的恒等变换及化简求值,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:计算题,三角函数的求值
分析:(1)依题意,其最小正周期为π,易求ω=2,又y=f(x)的图象经过点(
,1),-
<φ<
,可求得φ=
,从而可得f(x)的解析式;
(2)由f(α)+f(α-
)=
,可求得sin2α=
,又α为锐角,从而可得sinα+cosα的值.
| π |
| 12 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
(2)由f(α)+f(α-
| π |
| 3 |
| 24 |
| 25 |
| 24 |
| 25 |
解答:
解:(1)∵f(x)的最小正周期为π,ω>0,
∴
=π,ω=2,
又y=f(x)的图象经过点(
,1),
∴2×
+φ=2kπ+
,
∴φ=2kπ+
(k∈Z),又-
<φ<
,
∴φ=
,
∴f(x)=sin(2x+
).
(2)∵f(α)+f(α-
)=
,
∴sin(2α+
)+sin(2α-
)=
,
整理得sin2α=
,即(sinα+cosα)2=1+
=
,
又α为锐角,inα+cosα>0,
∴sinα+cosα=
.
∴
| 2π |
| ω |
又y=f(x)的图象经过点(
| π |
| 12 |
∴2×
| π |
| 12 |
| π |
| 2 |
∴φ=2kπ+
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
∴φ=
| π |
| 3 |
∴f(x)=sin(2x+
| π |
| 3 |
(2)∵f(α)+f(α-
| π |
| 3 |
| 24 |
| 25 |
∴sin(2α+
| π |
| 3 |
| π |
| 3 |
| 24 |
| 25 |
整理得sin2α=
| 24 |
| 25 |
| 24 |
| 25 |
| 49 |
| 25 |
又α为锐角,inα+cosα>0,
∴sinα+cosα=
| 7 |
| 5 |
点评:本题考查三角函数的恒等变换及化简求值,考查由y=Asin(ωx+φ)的部分图象确定其解析式,属于中档题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
设变量x,y满足约束条件:
,则z=x+2y的最大值为( )
|
| A、21 | B、-3 | C、15 | D、-15 |
若P=
sinxdx,Q=
(-cosx)dx,R=
dx,则P,Q,R的大小关系是( )
| ∫ | π
|
| ∫ | π
|
| ∫ | π
|
| 1 |
| x |
| A、P=Q>R |
| B、P=Q<R |
| C、P>Q>R |
| D、P<Q<R |
已知函数f(x)=ax5+bx3+cx-2,且f (-12)=10,则f(12)=( )
| A、-14 | B、-12 |
| C、-10 | D、10 |
下列各数85(9)、1000(4)、111111(2)中最小的数是( )
| A、85(9) |
| B、111111(2) |
| C、1000(4) |
| D、不确定 |
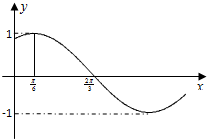 已知函数
已知函数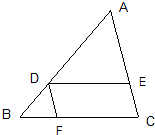 (几何证明选讲选做题)如图,在△ABC中,DE∥BC,DF∥AC,AE=4,EC=2,BC=8,则BF=
(几何证明选讲选做题)如图,在△ABC中,DE∥BC,DF∥AC,AE=4,EC=2,BC=8,则BF=