题目内容
4.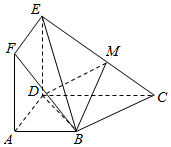 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,$AB=AD=\frac{1}{2}CD=2$,$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$.
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,$AB=AD=\frac{1}{2}CD=2$,$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$.(1)当$λ=\frac{1}{2}$时,求证:BM∥平面ADEF;
(2)若平面BDM与平面ABF所成锐角二面角的余弦值为$\frac{1}{{\sqrt{38}}}$时,求λ的值.
分析 (1)取DE中点N,连结MN,AN,则由中位线定理可得BM∥AN,从而BM∥平面ADEF;
(2)建立空间坐标系,求出平面ABF和平面BDM的法向量,根据法向量夹角与二面角的关系列方程解出λ.
解答  证明:(1)取DE中点N,连结MN,AN,
证明:(1)取DE中点N,连结MN,AN,
当λ=$\frac{1}{2}$时,M为EC中点,又N是DE中点,
∴MN∥CD,MN=$\frac{1}{2}CD$.
∵AB∥CD,AB=$\frac{1}{2}CD$,
∴AB∥MN,AB=MN.
∴四边形ABMN是平行四边形,
∴BM∥AN,∵AN?平面ADEF,BM?平面ADEF,
∴BM∥平面ADEF.
(2)以D为坐标原点建立空间坐标系如图:
则$\overrightarrow{AD}$为平面ABF的一个法向量,$\overrightarrow{AD}=(-2,0,0)$.
$\overrightarrow{DB}=(2,2,0)$,$\overrightarrow{DM}$=(0,4λ,2-2λ).
设$\overrightarrow{n}$=(x,y,z)为平面BDM的一个法向量,
则$\left\{\begin{array}{l}{2x+2y=0}\\{4λy+2z-2λz=0}\end{array}\right.$,令z=1,得$\overrightarrow{n}$=($\frac{2-2λ}{4λ}$,$\frac{2λ-2}{4λ}$,1).
∴cos<$\overrightarrow{AD},\overrightarrow{n}$>=$\frac{\overrightarrow{AD}•\overrightarrow{n}}{|\overrightarrow{AD}||\overrightarrow{n}|}$=$\frac{λ-1}{\sqrt{6{λ}^{2}-4λ+2}}$=-$\frac{1}{\sqrt{38}}$.
解得$λ=\frac{3}{2}$(舍)或λ=$\frac{3}{4}$.
点评 本题考查了线面平行的判定,二面角的求法,属于中档题.

| A. | π | B. | 2π | C. | 4π | D. | 0 |
| A. | $\frac{\sqrt{2}}{10}$ | B. | -$\frac{\sqrt{2}}{10}$ | C. | $\frac{7\sqrt{2}}{10}$ | D. | -5 |
| A. | (-∞,-$\frac{9}{4}$] | B. | (-2,+∞) | C. | [-$\frac{9}{4}$,+∞) | D. | [4,+∞) |
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $-\sqrt{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |