题目内容
14.$\frac{{tan{{27}°}+tan{{213}°}}}{{1-tan{{27}°}tan{{33}°}}}$=( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $-\sqrt{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
分析 由条件利用诱导公式、两角和的正切公式,求得要求式子的值.
解答 解:$\frac{{tan{{27}°}+tan{{213}°}}}{{1-tan{{27}°}tan{{33}°}}}$=$\frac{tan27°+tan33°}{1-tan27°tan33°}$=tan60°=$\sqrt{3}$,
故选:B.
点评 本题主要考查诱导公式、两角和的正切公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知函数$f(x)=\left\{\begin{array}{l}{({\frac{1}{2}})^x},x≤0\\{log_2}({x+2}),x>0\end{array}\right.$,若f(x0)=2,则x0=( )
| A. | 2或-1 | B. | 2 | C. | -1 | D. | 2或1 |
19.若圆C的方程为(x-3)2+(y-2)2=4,直线l的方程为x-y+1=0,则圆C关于直线l对称的圆的方程为( )
| A. | (x+1)2+(y+4)2=4 | B. | (x-1)2+(y-4)2=4 | C. | (x-4)2+(y-1)2=4 | D. | (x+4)2+(y+1)2=4 |
6.在三棱锥S-ABC中,E,F分别为SB,SC上的点,且EF∥面ABC,则( )
| A. | EF与BC相交 | B. | EF∥BC | C. | EF与BC异面 | D. | 以上均有可能 |
3.已知函数$f(x)=\left\{{\begin{array}{l}{({2a-1})x+2a,x<1}\\{{{log}_a}x,x≥1}\end{array}}\right.$是R上的减函数,则实数a的取值范围是( )
| A. | $(0,\frac{1}{2})$ | B. | [$\frac{1}{4},\frac{1}{2}$) | C. | ($\frac{1}{4},\frac{1}{2}$) | D. | ($0,\frac{1}{4}$) |
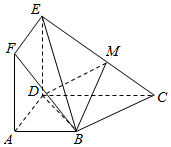 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,$AB=AD=\frac{1}{2}CD=2$,$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$.
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,$AB=AD=\frac{1}{2}CD=2$,$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$.