题目内容
14.已知cos(α+$\frac{π}{4}$)=-$\frac{4}{5}$($\frac{π}{4}$<α<$\frac{3π}{4}$),则cosα等于( )| A. | $\frac{\sqrt{2}}{10}$ | B. | -$\frac{\sqrt{2}}{10}$ | C. | $\frac{7\sqrt{2}}{10}$ | D. | -5 |
分析 利用两角和差的余弦公式进行求解即可.
解答 解:∵$\frac{π}{4}$<α<$\frac{3π}{4}$,
∴$\frac{π}{2}$<α+$\frac{π}{4}$<π,
则sin(α+$\frac{π}{4}$)=$\sqrt{1-(-\frac{4}{5})^{2}}$=$\frac{3}{5}$,
则cosα=cos[(α+$\frac{π}{4}$)-$\frac{π}{4}$]=cos(α+$\frac{π}{4}$)cos$\frac{π}{4}$+sin(α+$\frac{π}{4}$)sin$\frac{π}{4}$=-$\frac{4}{5}$×$\frac{\sqrt{2}}{2}$+$\frac{3}{5}$×$\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{2}}{10}$,
故选:B.
点评 本题主要考查三角函数值的计算,利用两角和差的余弦公式是解决本题的关键.考查学生的计算能力.

练习册系列答案
相关题目
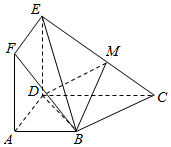 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,$AB=AD=\frac{1}{2}CD=2$,$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$.
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,$AB=AD=\frac{1}{2}CD=2$,$\overrightarrow{EM}=λ\overrightarrow{EC}(0<λ<1)$.