题目内容
已知正四棱锥V-ABCD的侧棱长与底面边长都相等,E是VA的中点,O为底面中心,则异面直线EO、BC所成的角是 .
考点:异面直线及其所成的角
专题:空间角
分析:由题意画出图形,利用作平行线的方法找到异面直线所成的角,然后求之.
解答:
解:如图,
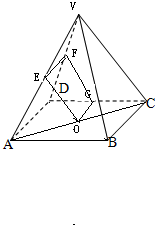
过E作EF∥AD,OG∥AD,
因为正四棱锥V-ABCD的侧棱长与底面边长都相等,E是VA的中点,O为底面中心,
所以F,G分别是VD,CD的中点,所以EF=OG=
BC,EF∥OG∥BC,
所以EO与BC所成的角等于EF与OE所成的角,
∴∠FGO是异面直线EO与BC所成的角.
∵正四棱锥V-ABCD的侧棱长与底面边长都相等,
∴FG=OG=
BC,△VCB为等边三角形,∠VCB=60°,
∴∠FGO=60°,
∴异面直线EO与BC所成的角为60°.
故答案为:60°.

过E作EF∥AD,OG∥AD,
因为正四棱锥V-ABCD的侧棱长与底面边长都相等,E是VA的中点,O为底面中心,
所以F,G分别是VD,CD的中点,所以EF=OG=
| 1 |
| 2 |
所以EO与BC所成的角等于EF与OE所成的角,
∴∠FGO是异面直线EO与BC所成的角.
∵正四棱锥V-ABCD的侧棱长与底面边长都相等,
∴FG=OG=
| 1 |
| 2 |
∴∠FGO=60°,
∴异面直线EO与BC所成的角为60°.
故答案为:60°.
点评:本题考查了异面直线所成的角,关键是利用四棱锥的性质将空间角转化为平面角,利用等边三角形的性质解答,属于常考题.

练习册系列答案
相关题目
将3张不同的奥运门票分给10名同学中的3人,每人1张,则不同的分法有( )
| A、2610种 | B、720种 |
| C、240种 | D、60种 |
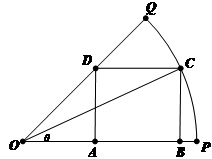 如图,在半径为40cm、圆心角为60°的扇形铝皮OPQ上截取一块矩形材料ABCD,其中点A,B在OP上,点C在
如图,在半径为40cm、圆心角为60°的扇形铝皮OPQ上截取一块矩形材料ABCD,其中点A,B在OP上,点C在
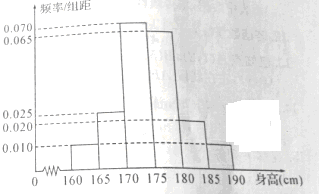 为了调查某校高三男生的身高和相关的运动指标,在该校高三男学生中随机抽取了若干名同学作为样本,测得他们的身高后,画出频率分布直方图如图所示,若185~190身高段的人数为2人.
为了调查某校高三男生的身高和相关的运动指标,在该校高三男学生中随机抽取了若干名同学作为样本,测得他们的身高后,画出频率分布直方图如图所示,若185~190身高段的人数为2人.