题目内容
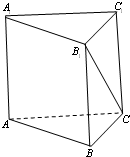 如图,正三棱柱的底面边长为1,体积为
如图,正三棱柱的底面边长为1,体积为| 3 |
考点:异面直线及其所成的角
专题:空间角
分析:根据已知条件容易求得BB1=4,并且判断出∠BB1C是异面直线A1A与B1C所成的角,而tan∠BB1C=
,所以得到异面直线A1A与B1C所成的角的大小为arctan
.
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:根据已知条件知,
•1•1•sin60°•BB1=
;
∴BB1=4;
∵BB1∥AA1;
∴∠BB1C是异面直线A1A与B1C所成角;
∴在Rt△BCB1中,tan∠BB1C=
;
∴∠BB1C=arctan
.
故答案为:arctan
.
| 1 |
| 2 |
| 3 |
∴BB1=4;
∵BB1∥AA1;
∴∠BB1C是异面直线A1A与B1C所成角;
∴在Rt△BCB1中,tan∠BB1C=
| 1 |
| 4 |
∴∠BB1C=arctan
| 1 |
| 4 |
故答案为:arctan
| 1 |
| 4 |
点评:考查三角形面积公式,三棱柱的体积公式,以及异面直线所成角的概念及求法.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知sin10°=k,则cos620°等于( )
| A、k | ||
| B、-k | ||
| C、±k | ||
D、
|
已知α,β为锐角,
+
=2,则有( )
| sinα |
| cosβ |
| sinβ |
| cosα |
A、α+β>
| ||
B、α+β=
| ||
C、α+β<
| ||
D、α+β=
|
函数y=
的定义域为( )
| ||
| ln(1-x) |
| A、(0,1) |
| B、[0,1) |
| C、(0,1] |
| D、[0,1] |
若(a-3)-3<(1+2a)-3,则实数a的取值范围是( )
| A、(-4,+∞) | ||
B、{a|a>-4,a≠3且a≠-
| ||
| C、(-∞,-4) | ||
D、(-∞,-4)∪(-
|
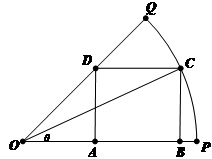 如图,在半径为40cm、圆心角为60°的扇形铝皮OPQ上截取一块矩形材料ABCD,其中点A,B在OP上,点C在
如图,在半径为40cm、圆心角为60°的扇形铝皮OPQ上截取一块矩形材料ABCD,其中点A,B在OP上,点C在