题目内容
已知函数f（x）中，f（1）=0，且对任意正整数x满足f（x+1）=f（x）+2x，则f（2012）=（ ）
| A、2010×2011 |
| B、20112 |
| C、2011×2012 |
| D、20122 |
考点：函数的值
专题：函数的性质及应用
分析：由已知得f（2012）=f（1）+2（1+2+3+…+2011），由此能求出结果．
解答：
解：∵函数f（x）中，f（1）=0，
且对任意正整数x满足f（x+1）=f（x）+2x，
∴f（2012）=f（1）+2（1+2+3+…+2011）
=0+2×
=2011×2012．
故选：C．
且对任意正整数x满足f（x+1）=f（x）+2x，
∴f（2012）=f（1）+2（1+2+3+…+2011）
=0+2×
| 2011(1+2011) |
| 2 |
=2011×2012．
故选：C．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
函数f（x）=x-
是（ ）
| 1 |
| x |
| A、奇函数 |
| B、偶函数 |
| C、非奇非偶函数 |
| D、既是奇函数又是偶函数 |
设i是虚数单位，复数
（ ）
| 7+4i |
| 1+2i |
| A、3-2i | B、3+2i |
| C、2-3i | D、2+3i |
已知α，β为锐角，
+
=2，则有（ ）
| sinα |
| cosβ |
| sinβ |
| cosα |
A、α+β＞
| ||
B、α+β=
| ||
C、α+β＜
| ||
D、α+β=
|
函数y=
的定义域为（ ）
| ||
| ln(1-x) |
| A、（0，1） |
| B、[0，1） |
| C、（0，1] |
| D、[0，1] |
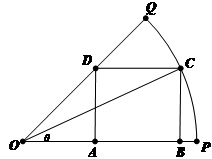如图，在半径为40cm、圆心角为60°的扇形铝皮OPQ上截取一块矩形材料ABCD，其中点A，B在OP上，点C在