题目内容
6.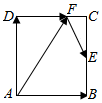 如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.
如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.
分析 以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立直角坐标系,可得A(0,0),B($\sqrt{3}$,0),D(0,2),E($\sqrt{3}$,1),设F(t,2),运用向量的数量积的坐标表示,可得t=1,再由向量的加减运算,计算即可得到所求值.
解答 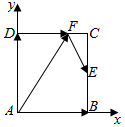 解:以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立直角坐标系,
解:以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立直角坐标系,
可得A(0,0),B($\sqrt{3}$,0),D(0,2),E($\sqrt{3}$,1),设F(t,2),
由$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,可得$\sqrt{3}$t=$\sqrt{3}$,解得t=1,
即F(1,2),$\overrightarrow{DF}$=(1,0),$\overrightarrow{AD}$=(0,2),$\overrightarrow{FE}$=($\sqrt{3}$-1,-1),
则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$=(1,-2)•($\sqrt{3}$-1,-1)
=$\sqrt{3}$-1+2=1+$\sqrt{3}$.
故答案为:1+$\sqrt{3}$.
点评 本题考查向量的数量积的运算,注意运用坐标表示,考查向量的加减运算,属于基础题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
14.已知a,b,c∈R,则“a>0且b2-4ac<0”是“?x∈R,都有ax2+bx+c≥0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.已知集合A={x|-1≤x<2},B={x|1<x<4},则A∪B可表示为( )
| A. | [-1,4) | B. | (-1,4) | C. | [-1,1) | D. | (1,2) |
11.某程序框图如图所示,则该程序运行后输出的值是( )


| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
15.已知M=a+$\frac{1}{a-1}$(a>1),N=3${\;}^{1-{x}^{2}}$(x∈R),则M,N的大小关系为( )
| A. | M≥N | B. | M>N | C. | M<N | D. | M≤N |