题目内容
18.定义数列如下:a1=2,an+1=an2-an+1,n∈N*.求证:(1)对于n∈N*恒有an+1>an成立;
(2)1-$\frac{1}{{2}^{2016}}$<$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$<1.
分析 (1)作差法化简an+1-an=an2-2an+1=(an-1)2,从而证明;
(2)化简an+1=an2-an+1可得$\frac{1}{{a}_{n+1}-1}$=$\frac{1}{{a}_{n}({a}_{n}-1)}$=$\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n}}$,从而可得$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n+1}-1}$,从而求和,再证明不等式即可.
解答 证明:(1)∵an+1=an2-an+1,
∴an+1-an=an2-2an+1=(an-1)2≥0,
又∵a1=2,∴an+1-an>0,
∴对于n∈N*恒有an+1>an成立;
(2)∵an+1=an2-an+1,
∴an+1-1=an2-an,
即$\frac{1}{{a}_{n+1}-1}$=$\frac{1}{{a}_{n}({a}_{n}-1)}$=$\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n}}$,
∴$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{n}-1}$-$\frac{1}{{a}_{n+1}-1}$,
$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$=($\frac{1}{{a}_{1}-1}$-$\frac{1}{{a}_{2}-1}$)+($\frac{1}{{a}_{2}-1}$-$\frac{1}{{a}_{3}-1}$)+…+($\frac{1}{{a}_{2016}-1}$-$\frac{1}{{a}_{2017}-1}$)
=$\frac{1}{{a}_{1}-1}$-$\frac{1}{{a}_{2017}-1}$=1-$\frac{1}{{a}_{2017}-1}$<1,
∵an+1-1=an2-an,
∴$\frac{{a}_{n+1}-1}{{a}_{n}-1}$=an≥2(当且仅当n=1时,等号成立),又∵a1-1=1,
∴a2017-1>22016,
故1-$\frac{1}{{2}^{2016}}$<1-$\frac{1}{{a}_{2017}-1}$,
故1-$\frac{1}{{2}^{2016}}$<$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$<1.
点评 本题考查了作差法的应用及构造法及裂项求和法的应用,属于中档题.

| A. | -20 | B. | -15 | C. | 15 | D. | 20 |
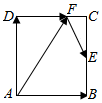 如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.
如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.