题目内容
16.在等比数列{an}中,(1)a4=2,a7=8,求an;
(2)a2+a5=18,a3+a6=9,an=1,求n.
分析 (1)由已知求得公比,进一步求出首项,代入等比数列的通项公式得答案;
(2)由已知求得公比,进一步求出首项,代入等比数列的通项公式求得n值.
解答 解:(1)在等比数列{an}中,由a4=2,a7=8,
得${q}^{3}=\frac{{a}_{7}}{{a}_{4}}=\frac{8}{2}=4$,∴$q=\root{3}{4}$,
则${a}_{1}=\frac{{a}_{4}}{q}=\frac{2}{\root{3}{4}}=\root{3}{2}$,
则${a}_{n}=\root{3}{2}•(\root{3}{4})^{n-1}={2}^{\frac{2n-1}{3}}$;
(2)由a2+a5=18,a3+a6=9,
得$q=\frac{{a}_{3}+{a}_{6}}{{a}_{2}+{a}_{5}}=\frac{9}{18}=\frac{1}{2}$,
代入${a}_{1}q+{a}_{1}{q}^{4}=18$,得${a}_{1}(\frac{1}{2}+\frac{1}{16})=18$,即a1=32.
由an=${a}_{1}{q}^{n-1}=32•(\frac{1}{2})^{n-1}=1$,得n=6.
点评 本题考查等比数列的通项公式,考查了等比数列的性质,是基础的计算题.

练习册系列答案
相关题目
6.已知a,b,c为不全相等的实数,P=a2+b2+c2+3,Q=2(a+b+c),那么P与Q的大小关系是( )
| A. | P>Q | B. | P≥Q | C. | P<Q | D. | P≤Q |
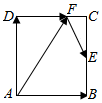 如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.
如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.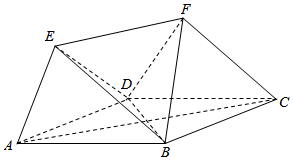 如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.
如图,多面体ABCDEF中,四边形ABCD为菱形,且∠DAB=60°,EF∥AC,AD=2,EA=ED=EF=$\sqrt{3}$.