题目内容
17.已知各项均为正数的数列{an}前n项和为Sn,若${S_1}=2{,_{\;}}3{S_n}^2-2{a_{n+1}}{S_n}=a_{n+1}^2$,则an=$\left\{\begin{array}{l}{2,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$.分析 把已知数列递推式变形,可得$\frac{{a}_{n+1}}{{a}_{n}}=2$(n≥2),即数列{an}从第二项起构成以2为公比的等比数列,再由等比数列的通项公式求得答案.
解答 解:由S1=2,得a1=S1=2,
由$3{{S}_{n}}^{2}-2{a}_{n+1}{S}_{n}={{a}_{n+1}}^{2}$,
得$4{{S}_{n}}^{2}=({S}_{n}+{a}_{n+1})^{2}$,
又an>0,
∴2Sn=Sn+an+1,即Sn=an+1,
当n≥2时,Sn-1=an,
两式作差得:an=an+1-an,即$\frac{{a}_{n+1}}{{a}_{n}}=2$,
又由${S_1}=2{,_{\;}}3{S_n}^2-2{a_{n+1}}{S_n}=a_{n+1}^2$,求得a2=2,
∴当n≥2时,${a}_{n}={2}^{n-1}$.
验证n=1时不成立,
∴${a_n}=\left\{\begin{array}{l}2{,_{\;}}_{\;}n=1\\{2^{n-1}},n≥2\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{2,n=1}\\{{2}^{n-1},n≥2}\end{array}\right.$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了等比数列通项公式的求法,是中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
5.执行如图的程序框图,则输出S的值为( )


| A. | 2 | B. | -3 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{3}$ |
12.已知等差数列{an}的前n项和为Sn,a9=1,S18=0,当Sn取最大值时n的值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
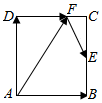 如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.
如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.