题目内容
15.已知M=a+$\frac{1}{a-1}$(a>1),N=3${\;}^{1-{x}^{2}}$(x∈R),则M,N的大小关系为( )| A. | M≥N | B. | M>N | C. | M<N | D. | M≤N |
分析 利用函数的单调性、基本不等式的性质即可得出.
解答 解:∵a>1,M=a+$\frac{1}{a-1}$=a-1+$\frac{1}{a-1}$+1≥2$\sqrt{(a-1)•\frac{1}{a-1}}$+1=3,当且仅当a=2时取等号.
∵x∈R,∴N=3${\;}^{1-{x}^{2}}$≤3.
∴M≥N.
故选:A.
点评 本题考查了函数的单调性、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5.执行如图的程序框图,则输出S的值为( )


| A. | 2 | B. | -3 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{3}$ |
3.二项式(1-x)6的展开式中x2的系数是( )
| A. | -20 | B. | -15 | C. | 15 | D. | 20 |
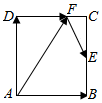 如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.
如图,在矩形ABCD中,AB=$\sqrt{3}$,BC=2,点E为BC的中点,点F在边CD上,若$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{3}$,则($\overrightarrow{DF}$-$\overrightarrow{AD}$)•$\overrightarrow{FE}$的值是1+$\sqrt{3}$.