题目内容
13.设关于x的方程x4-2x2=|x2-1|-k有f(k)个不同的实数根,且?k∈R,都有m>kf(k)恒成立,则实数m的取值范围是[10,+∞).分析 由题意可得x4-2x2-|x2-1|=-k,设g(x)=x4-2x2-|x2-1|,易得g(x)为偶函数,去绝对值画出图象,讨论-k的范围,即可得到根的个数,可得kf(k)<10.由恒成立思想即可得到m的范围.
解答 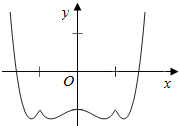 解:关于x的方程x4-2x2=|x2-1|-k即为
解:关于x的方程x4-2x2=|x2-1|-k即为
x4-2x2-|x2-1|=-k,
设g(x)=x4-2x2-|x2-1|,易得g(x)为偶函数,
当x2-1≥0即x≥1或x≤-1时,g(x)=x4-3x2+1
=(x2-$\frac{3}{2}$)2-$\frac{5}{4}$,当x2=$\frac{3}{2}$时取得最小值-$\frac{5}{4}$;
当x2-1<0即-1<x<1时,g(x)=x4-x2-1
=(x2-$\frac{1}{2}$)2-$\frac{5}{4}$,当x2=$\frac{1}{2}$时取得最小值-$\frac{5}{4}$.
函数y=g(x)的图象如图.
当-k>-1,即k<1时,f(k)=2;
当-k=-1,即k=1时,f(k)=5;
当-$\frac{5}{4}$<-k<-1,即1<k<$\frac{5}{4}$时,f(k)=8;
当-k=-$\frac{5}{4}$,即k=$\frac{5}{4}$时,f(k)=4;
当-k<-$\frac{5}{4}$,即k>$\frac{5}{4}$时,f(k)=0.
则kf(k)=$\left\{\begin{array}{l}{2k,k<1}\\{5,k=1,\frac{5}{4}}\\{8k,1<k<\frac{5}{4}}\\{0,k>\frac{5}{4}}\end{array}\right.$;
即有kf(k)<10.
由题意?k∈R,都有m>kf(k)恒成立,
即有m≥10.
则有m的范围是[10,+∞).
点评 本题考查函数恒成立问题的解法,考查函数方程的转化思想,考查数形结合的思想方法,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案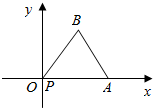 如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )| A. | (-$\frac{37}{3}$,-9) | B. | (-∞,-$\frac{37}{3}$) | C. | (-$\frac{37}{3}$,-5) | D. | (-9,-5) |
| A. | $\sqrt{6}$f($\frac{π}{6}$)$<\sqrt{3}$f($\frac{π}{4}$)$<\sqrt{2}$f($\frac{2π}{3}$) | B. | $\sqrt{6}$f($\frac{π}{6}$)$<\sqrt{2}$f($\frac{2π}{3}$)$<\sqrt{3}$f($\frac{π}{4}$) | C. | $\sqrt{2}$f($\frac{2π}{3}$)$<\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{6}$f($\frac{π}{6}$) | D. | $\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{6}$f($\frac{π}{6}$)$\sqrt{2}$f($\frac{2π}{3}$) |