题目内容
5.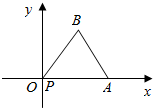 如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )| A. | (-$\frac{37}{3}$,-9) | B. | (-∞,-$\frac{37}{3}$) | C. | (-$\frac{37}{3}$,-5) | D. | (-9,-5) |
分析 确定f(4)=2,可得g(x),求导g′(x)=3x2+(m+4)x-2,从而转化为零点的存在性问题.
解答 解:根据题意画出顶点P(x,y)的轨迹,如图所示.轨迹是一段一段的圆弧组成的图形.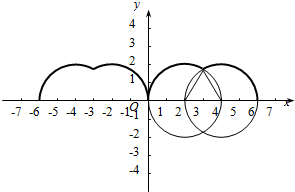
从图形中可以看出,f(4)=2,
∴g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]=g(x)=x3+(2+$\frac{m}{2}$)x2-2x,
∴g′(x)=3x2+(m+4)x-2;
∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2;
∴g′(t)<0,g′(3)>0;
由题意知:对于任意的t∈[1,2],g′(t)<0恒成立,
∴$\left\{\begin{array}{l}{g′(1)<0}\\{g′(2)<0}\\{g′(3)>0}\end{array}\right.$.
∴-$\frac{37}{3}$<m<-9,
故选:A.
点评 本题考查轨迹问题,考查导数知识的运用,考查学生分析解决问题的能力,确定函数的解析式是关键.

练习册系列答案
相关题目
 如图是一幅椭圆形彗星轨道图,长4cm,高2$\sqrt{3}$cm,已知O为椭圆的中心,A1,A2是长轴两端点,太阳位移椭圆的左焦点F处.
如图是一幅椭圆形彗星轨道图,长4cm,高2$\sqrt{3}$cm,已知O为椭圆的中心,A1,A2是长轴两端点,太阳位移椭圆的左焦点F处.