题目内容
1.设椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{9}$=1(a>3)的两个焦点分别为F1,F2.其离心率为$\frac{4}{5}$.椭圆上点M到F1的距离为2.点N是MF1的中点.O是椭圆的中心.求线段ON的长度.分析 根据体积求出a,利用椭圆的定义得|MF2|=10-2=8,ON是△MF1F2的中位线,由此能求出|ON|的值.
解答 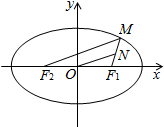 解:∵椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{9}$=1(a>3)的两个焦点分别为F1,F2.其离心率为$\frac{4}{5}$.
解:∵椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{9}$=1(a>3)的两个焦点分别为F1,F2.其离心率为$\frac{4}{5}$.
b=3,$\frac{c}{a}$=$\frac{4}{5}$,a2=9+c2,解得a=5,c=4,
椭圆的长轴长为2×5=10,
∴|MF2|=10-2=8,
ON是△MF1F2的中位线,
∴|ON|=$\frac{\left|{MF}_{2}\right|}{2}$=4,
线段ON的长度为:4.
点评 本题主要考查椭圆的简单性质、三角形的中位线,考查基础知识的灵活运用,作出草图数形结合效果更好.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.若复数z满足(z+1)i=2-i,则复数z的共轭复数在复平面上所对应点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.生产一定数量的商品的全部费用称为市生产成本,某企业一个月生产某种商品x万件时的生产成本为C(x)=$\frac{1}{2}$x2+2x+20(万元),每一万件售价是20万元,且生产的产品全部售完,则该企业一个月的利润Q(x)=( )
| A. | $\frac{1}{2}$x2-18x+20 | B. | -$\frac{1}{2}$x2+18x-20 | C. | $\frac{1}{2}$x2+2x | D. | $\frac{1}{2}$x2-18x |
 如图是一幅椭圆形彗星轨道图,长4cm,高2$\sqrt{3}$cm,已知O为椭圆的中心,A1,A2是长轴两端点,太阳位移椭圆的左焦点F处.
如图是一幅椭圆形彗星轨道图,长4cm,高2$\sqrt{3}$cm,已知O为椭圆的中心,A1,A2是长轴两端点,太阳位移椭圆的左焦点F处.