题目内容
2.过抛物线y2=2px(p>0)的焦点F的直线交抛物线于A,B两点,已知|AF|=3,|BF|=2,则p等于$\frac{12}{5}$.分析 根据AF|=3,|BF|=2,利用抛物线的定义可得A,B的横坐标,利用$\frac{{{y}_{1}}^{2}}{{{y}_{2}}^{2}}$=$\frac{{x}_{1}}{{x}_{2}}$=$\frac{9}{4}$,即可求得p的值.
解答 解:设A(x1,y1),B(x2,y2),则
∵|AF|=3,|BF|=2
∴根据抛物线的定义可得x1=3-$\frac{p}{2}$,x2=2-$\frac{p}{2}$,
∵$\frac{{{y}_{1}}^{2}}{{{y}_{2}}^{2}}$=$\frac{{x}_{1}}{{x}_{2}}$=$\frac{9}{4}$,
∴4(3-$\frac{p}{2}$)=9(2-$\frac{p}{2}$)
∴p=$\frac{12}{5}$.
故答案为:$\frac{12}{5}$.
点评 本题考查抛物线的定义,考查三角形的相似,解题的关键是利用抛物线的定义确定A,B的横坐标.

练习册系列答案
相关题目
13.有5位同学排成前后两排拍照,若前排站2人,则甲不站后排两端且甲、乙左右相邻的概率为( )
| A. | $\frac{3}{20}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{3}{5}$ |
17.在△ABC中,“A<B<C”是“cos2A>cos2B>cos2C”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
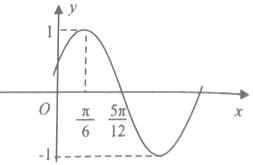 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,