题目内容
求函数f(x)=
mx2+2x+mlnx的单调区间.
| 1 |
| 2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:求导函数,对参数m进行讨论,即可确定函数f(x)的单调区间.
解答:
解:函数的定义域{x|x>0},f′(x)=mx+2+m•
=
令f′(x)=0,即mx2+2x+m=0
(1)当m=0时,f′(x)>0,则函数在定义域上为增函数;
(2)当△=4(1-m2)≤0,解得m≥1或m≤-1,
当m≥1时,f′(x)≥0,则函数在定义域上为增函数,
当m≤-1时,f′(x)≤0,则函数在定义域上为减函数;
(3)当0<m<1时,mx2+2x+m=0两根x1,x2(x1<x2)为负数,所以函数在定义域上为增函数
当-1<m<0时,mx2+2x+m=0两根x1,x2(x1<x2)异号
x1=
<0,x2=
>0
函数f(x)在(0,
)上为增函数,在(
,+∞)上为减函数.
综上所述:当m≥0时,函数y=f(x) 的增区间为(0,+∞);
当m≤-1时,函数y=f(x)的减区间(0,+∞);
当-1<m<0时,函数的增区间为(0,
),减区间为(
,+∞).
| 1 |
| x |
| mx2+2x+m |
| x |
令f′(x)=0,即mx2+2x+m=0
(1)当m=0时,f′(x)>0,则函数在定义域上为增函数;
(2)当△=4(1-m2)≤0,解得m≥1或m≤-1,
当m≥1时,f′(x)≥0,则函数在定义域上为增函数,
当m≤-1时,f′(x)≤0,则函数在定义域上为减函数;
(3)当0<m<1时,mx2+2x+m=0两根x1,x2(x1<x2)为负数,所以函数在定义域上为增函数
当-1<m<0时,mx2+2x+m=0两根x1,x2(x1<x2)异号
x1=
-1+
| ||
| m |
-1-
| ||
| m |
函数f(x)在(0,
-1-
| ||
| m |
-1-
| ||
| m |
综上所述:当m≥0时,函数y=f(x) 的增区间为(0,+∞);
当m≤-1时,函数y=f(x)的减区间(0,+∞);
当-1<m<0时,函数的增区间为(0,
-1-
| ||
| m |
-1-
| ||
| m |
点评:本题考查导数知识的运用,考查函数的单调区间,属于中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
已知集合A={x∈N|-1<x<2},B={x|2x≥1},则A∩B=( )
| A、∅ | B、{0} |
| C、{1} | D、{0,1} |
执行如图所示的程序框图,若输出的值为-105,则输入的n值可能为( )

| A、5 | B、7 | C、8 | D、10 |
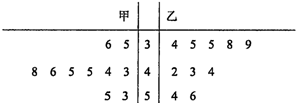
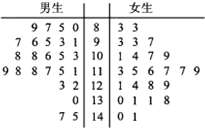 某校高三年级从一次模拟考试中随机抽取50名学生(男、女各25名),将数学成绩进行统计,所得数据的茎叶图如图所示.其中成绩在120分以上(含120分)为优秀.
某校高三年级从一次模拟考试中随机抽取50名学生(男、女各25名),将数学成绩进行统计,所得数据的茎叶图如图所示.其中成绩在120分以上(含120分)为优秀.