题目内容

把函数y=log2（x-2）+3的图象按向量
a
平移，得到函数y=log2（x+1）-1的图象，则
a
等于（　　）
A、（-3，-4）
B、（3，4）
C、（-3，4）
D、（3，-4）
考点：平面向量坐标表示的应用,函数的图象与图象变化
专题：平面向量及应用
分析：由y=log2（x-2）+3，得y-4=log2[（x-3）+1]-1，从而可得平移向量的坐标．
解答： 解：由y=log2（x-2）+3，得y-4=log2[（x-3）+1]-1，
∵函数y=log2（x-2）+3的图象按向量
a
平移，得到函数y=log2（x+1）-1的图象，
∴
a
=（-3，-4）．
故选A．
点评：本题考查函数图象的平移，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
等式lg（x+y）=lgx+lgy不是对数公式，但对某些x，y仍能成立，如x=y=2．试另举一例使等式成立．x=
 
，y=
 
．
在等差数列{an}中，a1=3，其前n项和为Sn，等比数列{bn}的各项均为正数，b1=1，公比为q（q≠0），且b2+S2=12，q=
S2
b2
．
（1）求{an}与{bn}的通项公式；
（2）证明：
1
3
≤
1
S1
+
1
S2
+…+
1
Sn
＜
2
3
．
函数f（x）=3cos
πx
2
-log
1
2
x零点个数是（　　）
A、2B、3C、4D、5
已知P是△ABC所在平面外一点，PA⊥PC，PB⊥PC，PA⊥PB．求证：P在面ABC上的射影H是△ABC的垂心．
有一个角为30°的三角板，斜边放在桌面内，三角板与桌面成30°的二面角，则三角板最短边所在的直线与桌面所成的角的正弦值为
 
．
已知
a
=（1，5，-1），
b
=（-2，3，5）．
（1）求
a
+
b
与
a
的夹角的余弦值；
（2）若（k
a
+
b
）∥（
a
-3
b
），求实数k的值；
（3）若（k
a
+
b
）⊥（
a
-3
b
），求实数k的值．
极坐标方程p=cosθ化为直角坐标方程是
 
．
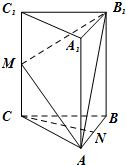如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=BC=2，AB=2
2
，CC1=4，M是棱CC1上一点．
（Ⅰ）求证：BC⊥AM；
（Ⅱ）若M，N分别为CC1，AB的中点，求证：CN∥平面AB1M．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网