题目内容
函数f(x)=3cos
-log
x零点个数是( )
| πx |
| 2 |
| 1 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
考点:根的存在性及根的个数判断,函数的零点
专题:函数的性质及应用
分析:在同一直角坐标系中画出函数f(x)=3cos
,g(x)=log
x的图象,令h(x)=f(x)-g(x),利用函数零点存在判定定理及函数的单调性即可判断出零点的个数.
| πx |
| 2 |
| 1 |
| 2 |
解答:
解:在同一直角坐标系中画出函数f(x)=3cos
,g(x)=log
x的图象,
令h(x)=f(x)-g(x),
①∵f(
)=3cos
<3,g(
)=3,f(
)=3cos
=
,g(
)=1,
∴h(
)<0,h(
)>0,∴h(
)h(
)<0,∴h(x)在区间(
,
)内存在零点;
②∵h(1)=f(1)-g(1)=0-0=0,∴x=1是函数h(x)的一个零点;
③∵h(2)=3cosπ-log
2=-3+1=-2<0,h(3)=3cos
-log
3=-log
3>0,
∴h(2)h(3)<0,h(x)在区间(2,3)内存在零点;
同理函数h(x)在区间(5,6),(6,7)内也分别存在零点.
④当x>8时,|f(x)|≤3,|g(x)|>|log
8|=3.∴函数h(x)在区间(8,+∞)上不存在零点.
综上可知:函数h(x)有且仅有5个零点.
故选D.
| πx |
| 2 |
| 1 |
| 2 |
令h(x)=f(x)-g(x),

①∵f(
| 1 |
| 8 |
| π |
| 16 |
| 1 |
| 8 |
| 1 |
| 2 |
| π |
| 4 |
3
| ||
| 2 |
| 1 |
| 2 |
∴h(
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
②∵h(1)=f(1)-g(1)=0-0=0,∴x=1是函数h(x)的一个零点;
③∵h(2)=3cosπ-log
| 1 |
| 2 |
| 3π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴h(2)h(3)<0,h(x)在区间(2,3)内存在零点;
同理函数h(x)在区间(5,6),(6,7)内也分别存在零点.
④当x>8时,|f(x)|≤3,|g(x)|>|log
| 1 |
| 2 |
综上可知:函数h(x)有且仅有5个零点.
故选D.
点评:熟练掌握函数零点存在判定定理及函数的单调性、数形结合的思想方法是解题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
若f(x)=x2+6,x∈[-1,2],则f(x)是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数,又是偶函数 |
| D、非奇非偶函数 |
已知a>b>c,下列不等式成立的是( )
| A、-a>-b | ||||
| B、a+c<b+c | ||||
| C、2a>2b | ||||
D、
|
已知(x+1)5(2x-1)3=a8x8+a7x7+…+a1x+a0,则a7的值为( )
| A、-2 | B、28 | C、43 | D、52 |
把函数y=log2(x-2)+3的图象按向量
平移,得到函数y=log2(x+1)-1的图象,则
等于( )
| a |
| a |
| A、(-3,-4) |
| B、(3,4) |
| C、(-3,4) |
| D、(3,-4) |
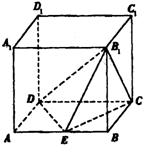 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点.设正方体的棱长为2a.
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点.设正方体的棱长为2a.