题目内容

已知P是△ABC所在平面外一点，PA⊥PC，PB⊥PC，PA⊥PB．求证：P在面ABC上的射影H是△ABC的垂心．
考点：直线与平面垂直的判定
专题：空间位置关系与距离
分析：利用向量的数量积公式，证明
AH
•
BC
=0，
BH
•
AC
=0，
CH
•
AB
=0，即可得到结论．
解答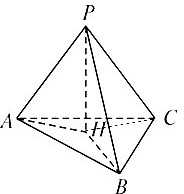： 证明：如图所示，连结AH、BH、CH，
∵PA⊥PC，PB⊥PC，PA⊥PB
∴
PA
•
PC
=0，
PB
•
PC
=0，
PA
•
PB
=0，
又∵PH⊥面ABC，
∴
PH
•
BC
=0，
PH
•
AB
=0，
PH
•
AC
=0，
∴
AH
•
BC
=（
PH
-
PA
）•
BC
=
PH
•
BC
-
PA
•
BC
=0-
PA
（
PC
-
PB
）=0-
PA
•
PC
+
PA
•
PB
=0．
同理可证：
BH
•
AC
=0，
CH
•
AB
=0．
∴H是△ABC的垂心．
点评：本题考查线面垂直、线线垂直，考查向量知识的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
平面上的两个向量
OA
，
OB
满足
|OA|
=a，
|OB|
=b，且
OA
⊥
OB
，a2+b2=4．向量：
OP
=x
OA
+y
OB
（x，y∈R），且a2(x-
1
2
)2+b2(y-
1
2
)2=1．
（1）如果点M为线段AB的中点，求证：
MP
=(x-
1
2
)
OA
+(y-
1
2
)
OB
；
（2）求丨
OP
丨的最大值，并求此时四边形OAPB面积的最大值．
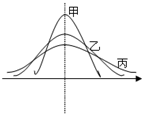某次市教学质量检测，甲、乙、丙三科考试成绩的直方图如图所示（由于人数众多，成绩分布的直方图可视为正态分布），则由图中曲线可得下列说法中正确的一个是（　　）
A、甲科总体的标准差最小
B、乙科总体的标准差及平均数都居中
C、丙科总体的平均数最小
D、甲、乙、丙的总体的平均数不相同
已知定义域为R的二次函数f（x）的最小值为0，且有f（1+x）=f（1-x），直线g（x）=4（x-1）的图象被f（x）的图象截得的弦长为4
17
，数列{an}满足a=2，（an+1-an）•g（an）+f（an）=0（n∈N*）．
（1）求函数f（x）的解析式；
（2）求数列{an}的通项公式；
（3）设bn=3f（an）-g（an），求数列的{bn}的最值及相应的n．
已知函数f（x）=
(
1
2
)x+
3
4
，x≥2
log2x，0＜x＜2
，若函数g（x）=f（x）-k有两个不同的零点，则实数k的取值范围是（　　）
A、（
3
4
，1）
B、（0，
3
4
）
C、（-∞，1）
D、（0，1）
把函数y=log2（x-2）+3的图象按向量
a
平移，得到函数y=log2（x+1）-1的图象，则
a
等于（　　）
A、（-3，-4）
B、（3，4）
C、（-3，4）
D、（3，-4）
在边长为a的正△ABC中，AD⊥BC于D，沿AD折成二面角B-AD-C后，BC=
1
2
a，这时二面角B-AD-C的大小为（　　）
A、30°B、45°
C、60°D、90°
直线y=
3
x被圆x2+y2-2x=0所截得的弦长是
 
．
一个几何体的三视图如图所示，正视图为正方形，俯视图为半圆，侧视图为矩形，则其表面积为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网