题目内容
在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q(q≠0),且b2+S2=12,q=
.
(1)求{an}与{bn}的通项公式;
(2)证明:
≤
+
+…+
<
.
| S2 |
| b2 |
(1)求{an}与{bn}的通项公式;
(2)证明:
| 1 |
| 3 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 2 |
| 3 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(1)利用等差数列的求和公式及等比数列的通项公式表示已知条件,然后解方程可求等比数列的公比q,等差数列的公差d,即可求解;
(2)利用裂项法求和,即可得到结论.
(2)利用裂项法求和,即可得到结论.
解答:
(1)解:设{an}的公差为d,
∵b2+S2=12,q=
∴q+6+d=12,q=
解得q=3或q=-4(舍),d=3
故an=3n,bn=3n-1;
(2)证明:Sn=
,∴
=
(
-
)
∴
+
+…+
=
(1-
+
-
+…
-
)=
•(1-
)
∵
≤1-
<1
∴
≤
•(1-
)<
∴
≤
+
+…+
<
.
∵b2+S2=12,q=
| S2 |
| b2 |
∴q+6+d=12,q=
| 6+d |
| q |
解得q=3或q=-4(舍),d=3
故an=3n,bn=3n-1;
(2)证明:Sn=
| n(3+3n) |
| 2 |
| 1 |
| Sn |
| 2 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 2 |
| 3 |
| 1 |
| n+1 |
∵
| 1 |
| 2 |
| 1 |
| n+1 |
∴
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| n+1 |
| 2 |
| 3 |
∴
| 1 |
| 3 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 2 |
| 3 |
点评:本题考查等差数列、等比数列的通项,考查裂项法求数列的和,考查数列与不等式的联系,属于中档题.

练习册系列答案
相关题目
已知a>b>c,下列不等式成立的是( )
| A、-a>-b | ||||
| B、a+c<b+c | ||||
| C、2a>2b | ||||
D、
|
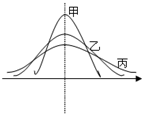 某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )
某次市教学质量检测,甲、乙、丙三科考试成绩的直方图如图所示(由于人数众多,成绩分布的直方图可视为正态分布),则由图中曲线可得下列说法中正确的一个是( )| A、甲科总体的标准差最小 |
| B、乙科总体的标准差及平均数都居中 |
| C、丙科总体的平均数最小 |
| D、甲、乙、丙的总体的平均数不相同 |
把函数y=log2(x-2)+3的图象按向量
平移,得到函数y=log2(x+1)-1的图象,则
等于( )
| a |
| a |
| A、(-3,-4) |
| B、(3,4) |
| C、(-3,4) |
| D、(3,-4) |
 已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).
已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).