题目内容
极坐标方程p=cosθ化为直角坐标方程是 .
考点:点的极坐标和直角坐标的互化
专题:计算题
分析:先将原极坐标方程ρ=cosθ两边同乘以ρ后化成直角坐标方程,再利用直角坐标方程进行判断.
解答:
解:将原极坐标方程ρ=cosθ,化为:
ρ2=ρcosθ,
化成直角坐标方程为:x2+y2-x=0,
即(x-
)2+y2=
.
故答案为:(x-
)2+y2=
.
ρ2=ρcosθ,
化成直角坐标方程为:x2+y2-x=0,
即(x-
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:(x-
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
已知a>b>c,下列不等式成立的是( )
| A、-a>-b | ||||
| B、a+c<b+c | ||||
| C、2a>2b | ||||
D、
|
把函数y=log2(x-2)+3的图象按向量
平移,得到函数y=log2(x+1)-1的图象,则
等于( )
| a |
| a |
| A、(-3,-4) |
| B、(3,4) |
| C、(-3,4) |
| D、(3,-4) |
在球O内任取一点P,则P点在球O的内接正四面体中的概率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等x|x|<x的解集是( )
| A、{x|0<x<1} |
| B、{x|-1<x<1} |
| C、{x|0<x<1}或{x|x<-1}, |
| D、{x|-1<x<0,x>1} |
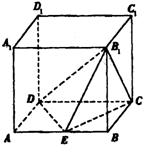 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点.设正方体的棱长为2a.
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点.设正方体的棱长为2a. 已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).
已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).