题目内容
下列各组函数是同一函数的是 （ ）
①f(x)=
与g(x)=x
；
②f（x）=x2-2x-1与g（t）=t2-2t-1；
③f（x）=x0与g(x)=
；
④f（x）=|x|与g(x)=(
)2．
①f(x)=
| -2x3 |
| -2x |
②f（x）=x2-2x-1与g（t）=t2-2t-1；
③f（x）=x0与g(x)=
| 1 |
| x0 |
④f（x）=|x|与g(x)=(
| x |
| A、①② | B、②③ | C、③④ | D、①④ |
考点：判断两个函数是否为同一函数
专题：函数的性质及应用
分析：根据函数的定义域相同，对应关系也相同的两个函数是同一函数，进行判断即可．
解答：
解：对于①，f(x)=
=-x
（x≤0），g(x)=x
（x≤0），它们的对应关系不同，不是同一函数；
对于②，f（x）=x2-2x-1（x∈R），g（t）=t2-2t-1（x∈R），它们的定义域相同，对应关系也相同，是同一函数；
对于③，f（x）=x0=1（x≠0），g(x)=
=1（x≠0），它们的定义域相同，对应关系也相同，是同一函数；
对于④，f（x）=|x|=
（x∈R），g(x)=(
)2=x（x≥0），它们的定义域不同，对应关系也不同，不是同一函数；
综上，是同一函数的为②③．
故选：B．
| -2x3 |
| -2x |
| -2x |
对于②，f（x）=x2-2x-1（x∈R），g（t）=t2-2t-1（x∈R），它们的定义域相同，对应关系也相同，是同一函数；
对于③，f（x）=x0=1（x≠0），g(x)=
| 1 |
| x0 |
对于④，f（x）=|x|=
|
| x |
综上，是同一函数的为②③．
故选：B．
点评：本题考查了判断两个函数是否为同一函数的问题，解题时应判断它们的定义域是否相同，对应关系是否也相同，是基础题．
练习册系列答案
相关题目
已知函数f（x），对任意的x∈R，满足f（-x）+f（x）=0，f（2-x）=f（x），且当x∈[0，1]时，f（x）=ax，若方程f（x）-lgx=0恰有五个实根，则实数a的取值范围是（ ）
| A、（-lg11，-lg7）∪（2lg3，lg13） |
| B、（-2lg3，-lg7）∪（lg11，lg13） |
| C、（-lg13，-lg11）∪（lg7，2lg3） |
| D、（-lg13，-2lg3）∪（lg7，lg11） |
下列函数中，最小正周期为2π的是（ ）
| A、y=cosx |
| B、y=sin（2x+π） |
| C、y=tanx |
| D、y=|sinx| |
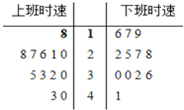某市对上下班交通情况作抽样调查，作出上下班时间各抽取的12辆机动车行驶时速（单位：km/h）的茎叶图如图．则上、下班行驶时速的中位数分别为（ ）| A、28与28.5 |
| B、29与28.5 |
| C、28与27.5 |
| D、29与27.5 |
为了了解某地区10000名高三男生的身体发育情况，抽查了该地区100名年龄为17～18岁的高三男生体重（kg），得到频率分布直方图如图．根据图示，请你估计该地区高三男生中体重在[56.5，64.5]kg的学生人数是（ ）